Rotate List
MediumGiven the head of a linked list, rotate the list to the right by k places.
Example 1:

Input: head = [1,2,3,4,5], k = 2 Output: [4,5,1,2,3]
Example 2:
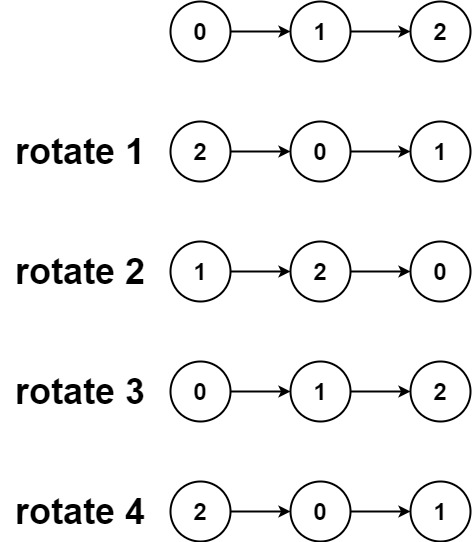
Input: head = [0,1,2], k = 4 Output: [2,0,1]
Constraints:
- The number of nodes in the list is in the range
[0, 500]. -100 <= Node.val <= 1000 <= k <= 2 * 109
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What is the range of values for `k`? Can `k` be negative or zero, or larger than the length of the list?
- Can the linked list be empty (i.e., `head` is null)? If so, what should I return?
- What is the data type and range of values stored in the nodes of the linked list? Can they be negative or zero?
- Should the original list be modified, or am I expected to create a new rotated list?
- Are there any memory constraints or concerns about creating a new linked list if the original list is very large?
Brute Force Solution
Approach
We want to rearrange a list of items by shifting them a certain number of positions. The most straightforward, though inefficient, way to do this is to repeatedly move items one position at a time until we've shifted them the required number of positions.
Here's how the algorithm would work step-by-step:
- Imagine you have a line of people, and you need to move everyone down the line a certain number of spots.
- To do this, you can take the last person in line and move them to the front.
- Do this repeatedly, one person at a time.
- Count how many times you've moved the last person to the front.
- Keep moving the last person to the front until you've done it the required number of times. The entire list has now been shifted.
Code Implementation
def rotate_list_brute_force(input_list, rotation_amount):
list_length = len(input_list)
# Handle cases where rotation is larger than list size
effective_rotation = rotation_amount % list_length
for _ in range(effective_rotation):
# Move the last element to the front of the list
last_element = input_list[-1]
# Necessary to shift the last element to the first position
for index in range(list_length - 1, 0, -1):
input_list[index] = input_list[index - 1]
input_list[0] = last_element
return input_listBig(O) Analysis
Optimal Solution
Approach
We need to shift the elements in a linked list, treating it like a circular arrangement. Instead of moving elements one by one, we'll find the new tail and head based on how much we need to shift the list.
Here's how the algorithm would work step-by-step:
- First, find the total number of elements in the list.
- Then, figure out the actual shift amount. Because it's circular, shifting by the number of elements (or a multiple of it) doesn't change anything, so adjust the shift amount to be within the range of the list's length.
- Next, identify the element that will become the new tail of the rotated list. This will be a certain number of elements before the original tail, determined by the shift amount.
- Reassign the connections: make the element before the new tail point to null, turning the new tail into the end of the list.
- Make the next element after the new tail the new head of the list.
- Finally, make the original tail point to the original head, linking the end back to the beginning and completing the rotation.
Code Implementation
class ListNode:
def __init__(self, val=0, next=None):
self.val = val
self.next = next
def rotate_right(head: ListNode, k: int) -> ListNode:
if not head:
return None
list_length = 1
tail = head
while tail.next:
tail = tail.next
list_length += 1
# Adjust shift amount to avoid unnecessary rotations.
effective_rotation = k % list_length
if effective_rotation == 0:
return head
# Find the new tail.
new_tail_position = list_length - effective_rotation
current = head
for i in range(1, new_tail_position):
current = current.next
new_tail = current
new_head = new_tail.next
# Break the list and connect the old tail to the old head.
new_tail.next = None
# Circular list creation.
tail.next = head
return new_headBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| head is null or empty list | Return null immediately as there's nothing to rotate. |
| List contains only one node | Return the head as is, since rotating a single-node list doesn't change it. |
| k is zero | Return the original head, as no rotation is needed. |
| k is a large number much greater than the list length | Calculate k % length to find the effective number of rotations to prevent unnecessary looping and potential integer overflow. |
| k is equal to the length of the list | Return the original head, as rotating by the list length results in the original list. |
| List contains a large number of nodes | The solution should iterate through the list only once to find the length and tail, and another time to find the new tail, ensuring linear time complexity O(n). |
| Negative k value | Convert k to its positive equivalent for proper rotation (k = length + (k % length)) to handle negative rotations. |
| Integer overflow when calculating length or k % length | Use appropriate data types (e.g., long) to prevent integer overflow when calculating the length of the linked list or performing modulo operations with large k values. |