Second Minimum Node In a Binary Tree #4 Most Asked
EasyGiven a non-empty special binary tree consisting of nodes with the non-negative value, where each node in this tree has exactly two or zero sub-node. If the node has two sub-nodes, then this node's value is the smaller value among its two sub-nodes. More formally, the property root.val = min(root.left.val, root.right.val) always holds.
Given such a binary tree, you need to output the second minimum value in the set made of all the nodes' value in the whole tree.
If no such second minimum value exists, output -1 instead.
Example 1:
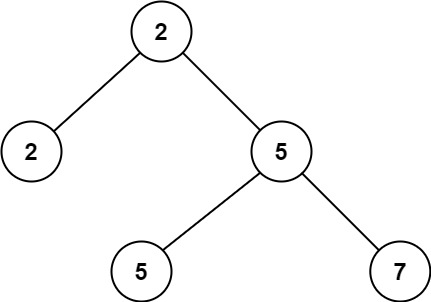
Input: root = [2,2,5,null,null,5,7] Output: 5 Explanation: The smallest value is 2, the second smallest value is 5.
Example 2:
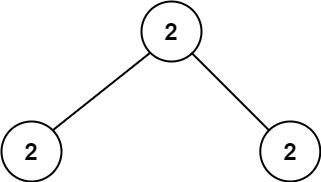
Input: root = [2,2,2] Output: -1 Explanation: The smallest value is 2, but there isn't any second smallest value.
Constraints:
- The number of nodes in the tree is in the range
[1, 25]. 1 <= Node.val <= 231 - 1root.val == min(root.left.val, root.right.val)for each internal node of the tree.
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What are the possible values for the node values in the tree? Are they guaranteed to be non-negative integers?
- Is the given binary tree guaranteed to be a special binary tree such that for every node, the value of the node is the minimum of the values of its children (if they exist)?
- What should I return if there is no second minimum node (i.e., all nodes have the same value)? Should I return null, -1, or throw an exception?
- Can the tree be empty or contain only one node? If so, what should I return?
- If the minimum value appears many times, should I consider the next smallest *distinct* value as the second minimum, or any value greater than the minimum?
Brute Force Solution
Approach
To find the second smallest value, we'll explore the entire tree without any shortcuts. We'll collect all the unique values and then find the second smallest among them.
Here's how the algorithm would work step-by-step:
- First, we need to look at every single value in the tree.
- As we examine each value, we will keep track of it in a collection.
- If we see a value we have already seen, we ignore it.
- Once we have looked at every single value in the tree, we have a list of all unique values.
- Then, we simply sort all the unique values from smallest to largest.
- The second value in the sorted list is the second smallest unique value in the tree.
Code Implementation
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
def find_second_minimum_value_brute_force(root):
unique_values = set()
def traverse_tree(node):
if not node:
return
# Collect all unique values in the tree.
unique_values.add(node.val)
traverse_tree(node.left)
traverse_tree(node.right)
traverse_tree(root)
# If there's only one unique value, there's no second minimum.
if len(unique_values) <= 1:
return -1
sorted_values = sorted(list(unique_values))
# The second element is the second smallest.
return sorted_values[1]Big(O) Analysis
Optimal Solution
Approach
The key to efficiently finding the second smallest value is understanding the binary tree's special property: each node's value is either equal to its parent's value or greater. This allows us to avoid checking unnecessary parts of the tree by keeping track of the smallest value and looking only for a value that's larger than the smallest but smaller than everything else.
Here's how the algorithm would work step-by-step:
- First, find the smallest value in the entire tree. This will be the value of the root node.
- Now, traverse the tree, but only explore branches where the node's value is greater than the smallest value we found earlier.
- As you explore, keep track of the smallest value you encounter that's also larger than the overall smallest value.
- If you find a value that meets these criteria, compare it to the current second smallest value you're tracking and update if necessary. If you don't find any such value after exploring the whole tree, it means there's no second smallest value.
Code Implementation
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
class Solution:
def findSecondMinimumValue(self, root):
smallest_value = root.val
second_smallest_value = float('inf')
def traverse(node):
nonlocal second_smallest_value
if not node:
return
# Only explore if the node's value is greater than the smallest.
if node.val > smallest_value:
second_smallest_value = min(second_smallest_value, node.val)
# Explore left and right subtrees recursively.
if node.val == smallest_value:
traverse(node.left)
traverse(node.right)
traverse(root)
# If second_smallest_value remains unchanged, there's no second smallest value.
if second_smallest_value == float('inf'):
return -1
return second_smallest_valueBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Null or empty tree | Return -1 immediately, as there's no second minimum. |
| Tree with only one node | Return -1, as there is no second minimum. |
| Tree with two nodes having same value | Return -1, as there is no second minimum. |
| All nodes in the tree have the same value | Return -1 because no second minimum exists. |
| The root node's value is also present in the subtree | The algorithm should correctly identify the second smallest value even with duplicate minimums. |
| Very large tree (potential stack overflow with recursion) | Use an iterative approach or a bounded recursive approach to avoid exceeding the maximum call stack size. |
| Integer overflow if node values are very large | Use a data type (e.g., long) that can accommodate large node values, and check for potential overflows when comparing. |
| The second minimum doesn't exist because all other values are larger | Handle by returning -1 if no value other than the minimum is found during traversal. |