Self Crossing #15 Most Asked
HardYou are given an array of integers distance.
You start at the point (0, 0) on an X-Y plane, and you move distance[0] meters to the north, then distance[1] meters to the west, distance[2] meters to the south, distance[3] meters to the east, and so on. In other words, after each move, your direction changes counter-clockwise.
Return true if your path crosses itself or false if it does not.
Example 1:
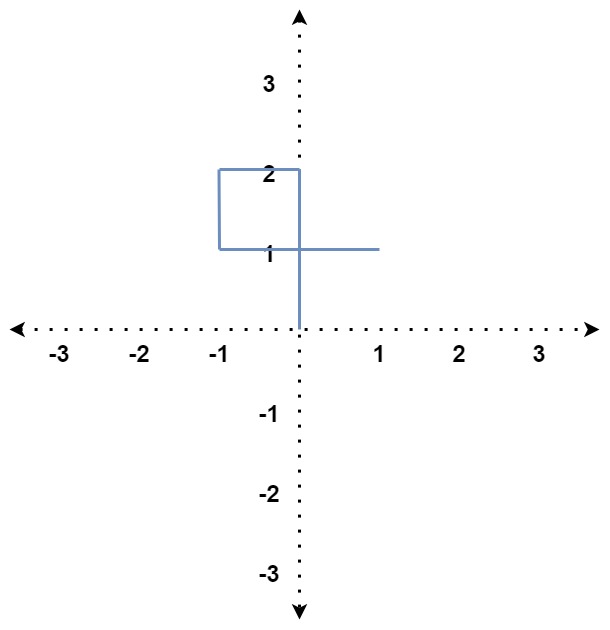
Input: distance = [2,1,1,2] Output: true Explanation: The path crosses itself at the point (0, 1).
Example 2:
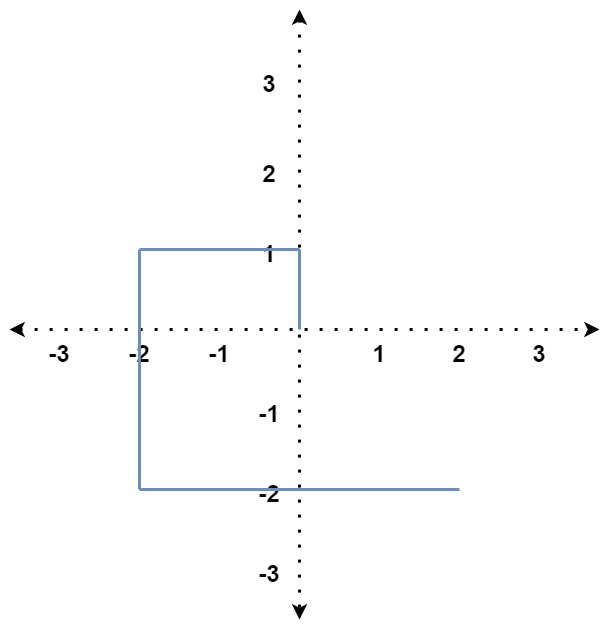
Input: distance = [1,2,3,4] Output: false Explanation: The path does not cross itself at any point.
Example 3:
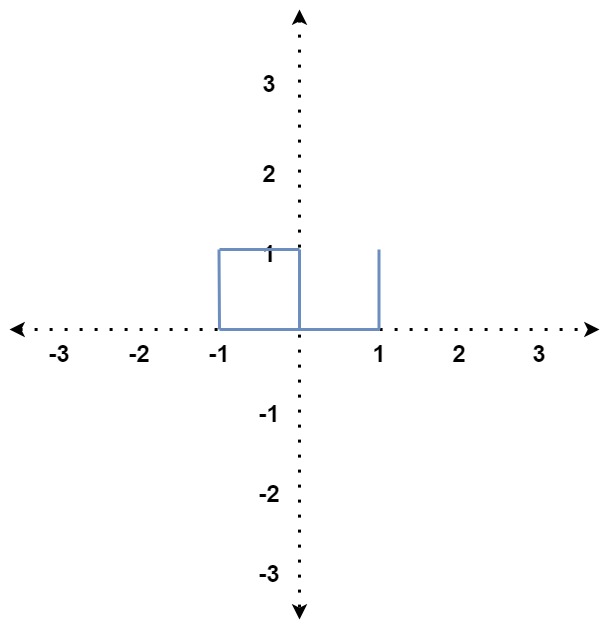
Input: distance = [1,1,1,2,1] Output: true Explanation: The path crosses itself at the point (0, 0).
Constraints:
1 <= distance.length <= 1051 <= distance[i] <= 105
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- Can the input array contain negative numbers, zeros, or floating-point numbers, or are we guaranteed positive integers?
- What is the expected length of the input array? Is there a maximum limit?
- If the path does not self-cross, should I return false or some other indicator like null?
- Should I consider a touch as a crossing or only a proper intersection of segments?
- Is the order of the input array significant, or could it be reordered without affecting whether a self-crossing occurs?
Brute Force Solution
Approach
Imagine you're drawing a path one step at a time. The brute force approach is to simply check after each step if the current step causes the path to cross over itself at any previous location. We do this by remembering every line segment we've drawn so far and checking if the newest one intersects any of them.
Here's how the algorithm would work step-by-step:
- Start drawing the path, one step at a time.
- After drawing each step, look back at every single line segment that you've drawn before.
- Check if the new line segment you just drew crosses any of the previous line segments.
- If the new line crosses any previous line, you've found a self-crossing path, and you're done.
- If the new line does not cross any previous line, keep drawing the path and repeating these checks until you have drawn all the steps.
- If you draw all the steps without finding any crossings, then there is no self-crossing.
Code Implementation
def is_self_crossing(distance): path = []
x_coordinate = 0
y_coordinate = 0
for step_distance in distance:
# Determine the next coordinate based on the current direction and distance
if len(path) % 4 == 0:
next_x_coordinate = x_coordinate
next_y_coordinate = y_coordinate + step_distance
elif len(path) % 4 == 1:
next_x_coordinate = x_coordinate - step_distance
next_y_coordinate = y_coordinate
elif len(path) % 4 == 2:
next_x_coordinate = x_coordinate
next_y_coordinate = y_coordinate - step_distance
else:
next_x_coordinate = x_coordinate + step_distance
next_y_coordinate = y_coordinate
new_segment = ((x_coordinate, y_coordinate), (next_x_coordinate, next_y_coordinate))
# Check for intersection with existing segments.
for index in range(len(path)):
existing_segment = path[index]
if do_intersect(new_segment, existing_segment):
return True
#Add the new segment to the path
path.append(new_segment)
x_coordinate = next_x_coordinate
y_coordinate = next_y_coordinate
return False
def orientation(point1, point2, point3):
value = (float(point2[1] - point1[1]) * (point3[0] - point2[0])) - \
(float(point2[0] - point1[0]) * (point3[1] - point2[1]))
if (value > 0):
return 1 # Clockwise
elif (value < 0):
return -1 # Counterclockwise
else:
return 0 # Collinear
def on_segment(point1, point2, point3):
if ( (point2[0] <= max(point1[0], point3[0])) and (point2[0] >= min(point1[0], point3[0])) and \
(point2[1] <= max(point1[1], point3[1])) and (point2[1] >= min(point1[1], point3[1]))):
return True
return False
def do_intersect(segment1, segment2):
point1, point2 = segment1
point3, point4 = segment2
orientation1 = orientation(point1, point2, point3)
orientation2 = orientation(point1, point2, point4)
orientation3 = orientation(point3, point4, point1)
orientation4 = orientation(point3, point4, point2)
# General case
if ((orientation1 != orientation2) and (orientation3 != orientation4)):
return True
# Special Cases
# point1, point2 and point3 are colinear and point3 lies on segment point1point2
if ((orientation1 == 0) and on_segment(point1, point3, point2)):
return True
# point1, point2 and point4 are colinear and point4 lies on segment point1point2
if ((orientation2 == 0) and on_segment(point1, point4, point2)):
return True
# point3, point4 and point1 are colinear and point1 lies on segment point3point4
if ((orientation3 == 0) and on_segment(point3, point1, point4)):
return True
# point3, point4 and point2 are colinear and point2 lies on segment point3point4
if ((orientation4 == 0) and on_segment(point3, point2, point4)):
return True
return FalseBig(O) Analysis
Optimal Solution
Approach
The core idea is to detect self-crossing by recognizing specific geometric patterns as we draw the path. We don't simulate the entire path; instead, we look for immediate crossing conditions by checking only a few previous steps.
Here's how the algorithm would work step-by-step:
- Imagine drawing a spiral path based on the input numbers, where each number is a segment length.
- As you draw each new line segment, check if it immediately causes a crossing with the previous few segments.
- Specifically, we look for five possible crossing scenarios that can happen with the previous three to five segments.
- The first scenario is when the current segment crosses the line two segments before it. This happens when the current segment is shorter or equal than the segment two steps back.
- The second scenario is when the current segment touches the line three steps back and the one step back is shorter or equal than three steps back and current step is greater or equal than the step before last.
- The third scenario is when the current segment crosses the line four segments back and the one segment back is shorter or equal than three steps back and the second step back is shorter or equal than the fourth step back.
- The fourth scenario is when the current segment touches the line five segments back and the one segment back is shorter or equal than three steps back and the second step back is shorter or equal than the fourth step back and the current step is greater or equal than the step before last.
- If any of these conditions are true during any step, it means the path crosses itself, and you can stop immediately and return true.
- If you complete the entire path without detecting any of these crossing scenarios, it means it doesn't cross itself, so you return false.
Code Implementation
def is_self_crossing(distance):
path_length = len(distance)
for i in range(3, path_length):
# Check for crossing with the line two steps back
if distance[i] >= distance[i - 2]:
return True
# Check for crossing with the line three steps back
if i >= 4 and distance[i - 1] == distance[i - 3] and distance[i] + distance[i - 4] >= distance[i - 2]:
return True
# Scenario 3: Crossing 4 segments back
if i >= 5 and distance[i - 1] <= distance[i - 3] and distance[i - 2] <= distance[i - 4] and distance[i] + distance[i - 4] >= distance[i - 2] and distance[i - 1] + distance[i - 5] >= distance[i - 3]:
return True
return FalseBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Null or empty input array | Return false immediately as no self-crossing is possible with no steps. |
| Array with fewer than 4 elements | Return false, as at least 4 moves are required to potentially form a self-crossing. |
| Array with only increasing values (e.g., [1,2,3,4,5]) | Return false as there's no chance of inward spiraling and crossing. |
| Immediate crossing, like [1, 1, 1, 1] | The core logic should detect and return true correctly. |
| Near misses, where the path gets very close but doesn't cross | Ensure sufficient precision in determining overlaps to avoid false negatives. |
| Large integer values in the input array, causing potential overflow in calculations. | Use appropriate data types (e.g., long) or modulo arithmetic to prevent integer overflow issues during coordinate calculations. |
| Spiral that extends very far before crossing | Ensure the solution's space complexity for storing path history doesn't become excessive, potentially by using a sliding window approach. |
| Input array with a large number of elements representing a very complex spiral | The solution's time complexity must remain reasonable; avoid brute force methods and prioritize efficient geometric checks. |