Shortest Cycle in a Graph #4 Most Asked
HardThere is a bi-directional graph with n vertices, where each vertex is labeled from 0 to n - 1. The edges in the graph are represented by a given 2D integer array edges, where edges[i] = [ui, vi] denotes an edge between vertex ui and vertex vi. Every vertex pair is connected by at most one edge, and no vertex has an edge to itself.
Return the length of the shortest cycle in the graph. If no cycle exists, return -1.
A cycle is a path that starts and ends at the same node, and each edge in the path is used only once.
Example 1:
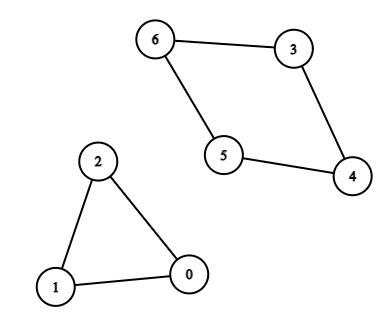
Input: n = 7, edges = [[0,1],[1,2],[2,0],[3,4],[4,5],[5,6],[6,3]] Output: 3 Explanation: The cycle with the smallest length is : 0 -> 1 -> 2 -> 0
Example 2:

Input: n = 4, edges = [[0,1],[0,2]] Output: -1 Explanation: There are no cycles in this graph.
Constraints:
2 <= n <= 10001 <= edges.length <= 1000edges[i].length == 20 <= ui, vi < nui != vi- There are no repeated edges.
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What is the maximum possible value for 'n', the number of nodes, and what is the maximum number of edges the graph can have?
- Are the node values represented by integers starting from 0 or 1, or can they be arbitrary?
- Can the graph be disconnected, or is it guaranteed to be a single connected component?
- If multiple shortest cycles exist, am I required to return a specific one, or can I return any of them?
- Are self-loops (an edge from a node to itself) or multi-edges (multiple edges between the same two nodes) allowed in the graph?
Brute Force Solution
Approach
To find the shortest cycle, we're going to check every possible path to see if it forms a cycle. We start from each point in the graph and explore all routes, looking for the shortest one that leads us back to where we started.
Here's how the algorithm would work step-by-step:
- Choose a starting point in the graph.
- Explore every possible path from that starting point, one step at a time.
- As we explore each path, keep track of the points we've visited.
- If a path ever leads us back to our starting point, we've found a cycle.
- Record the length of that cycle (how many steps it took to get back to the start).
- Repeat this process, starting from every other point in the graph.
- After checking all possible starting points and paths, compare all the cycle lengths we found.
- The shortest cycle length we found is the answer.
Code Implementation
def shortest_cycle_brute_force(graph):
shortest_cycle_length = float('inf')
for start_node in range(len(graph)):
# Iterate through each node as a potential start
for neighbor in range(len(graph)):
if graph[start_node][neighbor] == 1:
path = [start_node, neighbor]
queue = [(path)]
while queue:
current_path = queue.pop(0)
last_node = current_path[-1]
# Check for cycle if we returned to the start
if last_node == start_node and len(current_path) > 2:
shortest_cycle_length = min(shortest_cycle_length, len(current_path))
elif len(current_path) < len(graph):
# Limit max path length to prevent infinite loops
for next_node in range(len(graph)):
if graph[last_node][next_node] == 1 and next_node not in current_path:
new_path = current_path + [next_node]
queue.append((new_path))
if shortest_cycle_length == float('inf'):
return -1
else:
return shortest_cycle_length
Big(O) Analysis
Optimal Solution
Approach
To find the shortest cycle, we explore the graph starting from each point. We use a technique similar to searching for the nearest exit in a maze, keeping track of how far we've traveled and making sure we don't revisit places unnecessarily.
Here's how the algorithm would work step-by-step:
- Consider each point in the graph as a potential starting point for a cycle.
- From a chosen starting point, explore the graph step by step, noting the distance we've traveled from the start.
- If we ever encounter a point we've already visited during this exploration (other than the point we just came from), we've found a cycle.
- Calculate the length of this cycle based on the distances recorded.
- Keep track of the shortest cycle found so far.
- Repeat this process for every point in the graph.
- The shortest cycle found across all starting points is the solution.
Code Implementation
from collections import deque
def find_shortest_cycle(graph):
number_of_nodes = len(graph)
shortest_cycle_length = float('inf')
for start_node in range(number_of_nodes):
queue = deque([(start_node, -1, 0)])
distances = {start_node: 0}
while queue:
node, parent, distance = queue.popleft()
for neighbor in graph[node]:
if neighbor == parent:
continue
if neighbor in distances:
# Cycle detected, calculate cycle length.
cycle_length = distance + distances[neighbor] + 1
shortest_cycle_length = min(shortest_cycle_length, cycle_length)
else:
# Mark node visited with distance.
distances[neighbor] = distance + 1
queue.append((neighbor, node, distance + 1))
if shortest_cycle_length == float('inf'):
return -1
else:
return shortest_cycle_length
# Example usage:
if __name__ == '__main__':
graph_example_1 = {
0: [1, 2],
1: [0, 2],
2: [0, 1, 3],
3: [2]
}
graph_example_2 = {
0: [1, 2],
1: [0, 2, 3],
2: [0, 1],
3: [1]
}
graph_example_3 = {
0: [1],
1: [0, 2],
2: [1]
}
result_1 = find_shortest_cycle(graph_example_1)
print(f"Shortest cycle in graph_example_1: {result_1}")
result_2 = find_shortest_cycle(graph_example_2)
print(f"Shortest cycle in graph_example_2: {result_2}")
result_3 = find_shortest_cycle(graph_example_3)
print(f"Shortest cycle in graph_example_3: {result_3}")
Big(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Empty graph (n = 0, edges = []) | Return -1 immediately as an empty graph has no cycles. |
| Graph with only one node (n = 1, edges = []) | Return -1, as a single node cannot form a cycle. |
| Graph with two nodes and no edges (n = 2, edges = []) | Return -1, because two disconnected nodes cannot form a cycle. |
| Graph with two nodes and one edge (n = 2, edges = [[0, 1]]) | Return -1, as two nodes and one edge do not form a cycle. |
| Disconnected graph (multiple components) | The algorithm should explore each connected component independently and return the minimum cycle length found across all components or -1 if acyclic. |
| Graph with a self-loop (e.g., [0, 0]) | Handle self-loops by checking for 'next node == current node in BFS' or explicitly filtering during graph construction and return 1 since that is the shortest cycle. |
| Large graph (large n and many edges) | Ensure the algorithm uses a space-efficient representation of the graph (e.g., adjacency list) and that the BFS/DFS does not exceed memory limits or time constraints, possibly implement iterative deepening. |
| Graph with parallel edges between two nodes (e.g., [[0,1], [0,1]]) | The algorithm should treat parallel edges as a single edge when calculating the shortest cycle; multiple edges don't inherently create a smaller cycle. |