Shortest Path to Get All Keys

Hard

Asked by:

6 views

Topics:

GraphsDynamic Programming

You are given an m x n grid grid where:

'.' is an empty cell.
'#' is a wall.
'@' is the starting point.
Lowercase letters represent keys.
Uppercase letters represent locks.

You start at the starting point and one move consists of walking one space in one of the four cardinal directions. You cannot walk outside the grid, or walk into a wall.

If you walk over a key, you can pick it up and you cannot walk over a lock unless you have its corresponding key.

For some 1 <= k <= 6, there is exactly one lowercase and one uppercase letter of the first k letters of the English alphabet in the grid. This means that there is exactly one key for each lock, and one lock for each key; and also that the letters used to represent the keys and locks were chosen in the same order as the English alphabet.

Return the lowest number of moves to acquire all keys. If it is impossible, return -1.

Example 1:

Input: grid = ["@.a..","###.#","b.A.B"]
Output: 8
Explanation: Note that the goal is to obtain all the keys not to open all the locks.

Example 2:

Input: grid = ["@..aA","..B#.","....b"]
Output: 6

Example 3:

Input: grid = ["@Aa"]
Output: -1

Constraints:

m == grid.length
n == grid[i].length
1 <= m, n <= 30
grid[i][j] is either an English letter, '.', '#', or '@'.
There is exactly one '@' in the grid.
The number of keys in the grid is in the range [1, 6].
Each key in the grid is unique.
Each key in the grid has a matching lock.

Shortest Path to Get All Keys

Hard

Asked by:

6 views

Topics:

GraphsDynamic Programming

You are given an m x n grid grid where:

'.' is an empty cell.
'#' is a wall.
'@' is the starting point.
Lowercase letters represent keys.
Uppercase letters represent locks.

You start at the starting point and one move consists of walking one space in one of the four cardinal directions. You cannot walk outside the grid, or walk into a wall.

If you walk over a key, you can pick it up and you cannot walk over a lock unless you have its corresponding key.

For some 1 <= k <= 6, there is exactly one lowercase and one uppercase letter of the first k letters of the English alphabet in the grid. This means that there is exactly one key for each lock, and one lock for each key; and also that the letters used to represent the keys and locks were chosen in the same order as the English alphabet.

Return the lowest number of moves to acquire all keys. If it is impossible, return -1.

Example 1:

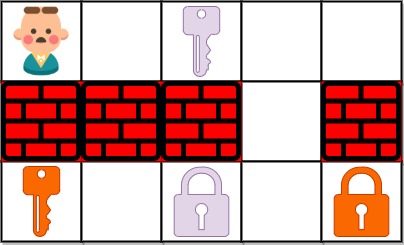
Input: grid = ["@.a..","###.#","b.A.B"]
Output: 8
Explanation: Note that the goal is to obtain all the keys not to open all the locks.

Example 2:

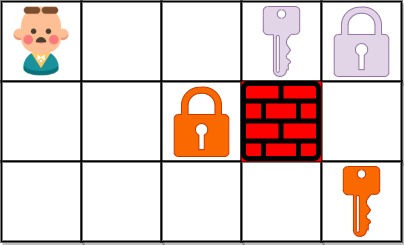
Input: grid = ["@..aA","..B#.","....b"]
Output: 6

Example 3:

Input: grid = ["@Aa"]
Output: -1

Constraints:

m == grid.length
n == grid[i].length
1 <= m, n <= 30
grid[i][j] is either an English letter, '.', '#', or '@'.
There is exactly one '@' in the grid.
The number of keys in the grid is in the range [1, 6].
Each key in the grid is unique.
Each key in the grid has a matching lock.

Solution

Clarifying Questions

When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:

What are the dimensions of the grid (rows and columns), and what are the maximum possible values?
What characters can appear in the grid besides '.', '#', '@', lowercase letters, and uppercase letters? Are empty grids possible?
If it's impossible to collect all the keys, what should I return?
Are the lowercase and uppercase letters guaranteed to be paired (i.e., for every key 'a', there's a corresponding lock 'A')?
Is it possible to start at a location where a key or lock is already present?

Brute Force Solution

Approach

The idea is to explore every possible path we can take through the maze. We keep going until we find the shortest one that lets us collect all the keys.

Here's how the algorithm would work step-by-step:

Start at the initial location.
Consider all possible moves: up, down, left, or right.
For each possible move, check if we can actually move there (is it a wall?).
If we can move there, move to the new location and check if we picked up a key or opened a lock.
Remember which keys we have at each location.
From the new location, again consider all possible moves and repeat the process.
If we reach a location where we have all the keys, note the number of moves it took.
Do this for every possible path we can take through the maze.
After exploring all possible paths, compare the number of moves for each path that collected all the keys and select the path with the fewest moves.

Code Implementation

def shortest_path_all_keys_brute_force(grid):
    rows = len(grid)
    columns = len(grid[0])
    start_row, start_column = -1, -1
    all_keys = 0

    # Find the starting position and calculate the total number of keys
    for row in range(rows):
        for column in range(columns):
            if grid[row][column] == '@':
                start_row, start_column = row, column
            elif 'a' <= grid[row][column] <= 'z':
                all_keys |= 1 << (ord(grid[row][column]) - ord('a'))

    shortest_path = float('inf')

    def explore(row, column, keys, moves):
        nonlocal shortest_path

        # Base case: If all keys are collected, update shortest path
        if keys == all_keys:
            shortest_path = min(shortest_path, moves)
            return

        if moves >= shortest_path:
            return

        # Define possible moves: up, down, left, right
        possible_moves = [(0, 1), (0, -1), (1, 0), (-1, 0)]

        for delta_row, delta_column in possible_moves:
            new_row, new_column = row + delta_row, column + delta_column

            # Boundary and wall check
            if 0 <= new_row < rows and 0 <= new_column < columns and grid[new_row][new_column] != '#':

                cell = grid[new_row][new_column]
                new_keys = keys

                # Key pickup
                if 'a' <= cell <= 'z':
                    key_index = ord(cell) - ord('a')
                    new_keys |= (1 << key_index)

                # Lock check
                if 'A' <= cell <= 'Z':
                    lock_index = ord(cell) - ord('A')
                    if not (keys & (1 << lock_index)):
                        continue

                # Explore the next possible state
                explore(new_row, new_column, new_keys, moves + 1)

    explore(start_row, start_column, 0, 0)

    if shortest_path == float('inf'):
        return -1
    else:
        return shortest_path

Try it yourself on LeetCode

Big(O) Analysis

Time Complexity

O(m*n*2^k) – The algorithm uses a breadth-first search (BFS) to explore the grid. Let m be the number of rows and n be the number of columns in the grid. The BFS visits each cell at most 2^k times, where k is the number of keys, because the state is defined by (row, column, keys_collected). For each cell, we consider 4 possible moves (up, down, left, right). Thus, the time complexity is O(m*n*2^k * 4), which simplifies to O(m*n*2^k).

Space Complexity

O(M * N * 2^K) – The space complexity is dominated by the queue used in the breadth-first search (BFS) to explore all possible paths. In the worst case, the queue can hold visited states. Each state consists of a row, column, and a bitmask representing the keys collected. Assuming an M x N grid, there are M * N possible locations. Since there can be at most K keys, the bitmask can have 2^K possible values. Therefore, the space required for the queue and visited set can grow up to O(M * N * 2^K), where K is the number of keys.

Optimal Solution

Approach

The problem is like navigating a maze where you need to collect all the keys before reaching the exit. The efficient approach uses a clever search to explore the maze, remembering which keys you've already found at each location to avoid unnecessary backtracking and find the shortest path.

Here's how the algorithm would work step-by-step:

Think of the maze as a series of rooms and hallways, and your goal is to visit all the rooms containing keys.
Start at the starting point and explore outwards, one step at a time. Keep track of all the places you've visited and the keys you have when you visit them.
When you encounter a locked door, check if you already have the key. If you do, open the door and continue exploring. If not, you'll need to find that key before coming back.
To avoid going around in circles, always prioritize exploring new areas. If you find yourself revisiting the same location with the same set of keys as before, you can ignore that path.
Continue exploring until you have found all the keys and reached the exit. The number of steps you took is the shortest path length.
The trick is to remember where you've been and which keys you had at each location so you don't repeat any unnecessary steps.

Code Implementation

def shortest_path_all_keys(grid):
    rows = len(grid)
    cols = len(grid[0])

    start_row, start_col = -1, -1
    all_keys = 0
    for row in range(rows):
        for col in range(cols):
            if grid[row][col] == '@':
                start_row, start_col = row, col
            elif 'a' <= grid[row][col] <= 'z':
                all_keys |= (1 << (ord(grid[row][col]) - ord('a')))

    queue = [(start_row, start_col, 0, 0)]
    visited = set()
    visited.add((start_row, start_col, 0))
    steps = 0

    while queue:
        length = len(queue)
        for _ in range(length):
            row, col, keys, distance = queue.pop(0)

            if keys == all_keys:
                return steps

            # Iterate through all possible directions.
            for delta_row, delta_col in [(0, 1), (0, -1), (1, 0), (-1, 0)]:
                new_row, new_col = row + delta_row, col + delta_col

                if 0 <= new_row < rows and 0 <= new_col < cols and grid[new_row][new_col] != '#':
                    cell = grid[new_row][new_col]

                    # If the cell is a lock.
                    if 'A' <= cell <= 'Z':
                        key_index = ord(cell) - ord('A')
                        if not (keys & (1 << key_index)):
                            continue

                    new_keys = keys
                    # If the cell is a key.
                    if 'a' <= cell <= 'z':
                        key_index = ord(cell) - ord('a')
                        new_keys |= (1 << key_index)

                    # This check prevents revisiting states.
                    if (new_row, new_col, new_keys) not in visited:
                        visited.add((new_row, new_col, new_keys))
                        queue.append((new_row, new_col, new_keys, distance))

        steps += 1

    return -1

Try it yourself on LeetCode

Big(O) Analysis

Time Complexity

O(m * n * 2^k) – Let m be the number of cells in the grid and n be the maximum number of neighbors for each cell, which is a constant in this problem (at most 4). k is the number of keys. We use a breadth-first search (BFS) to explore the grid. The size of the queue in BFS can be at most m * 2^k because each cell can be visited with different key combinations. For each cell in the queue, we explore its neighbors, which takes O(n) time. The total number of cells visited, considering key combinations, can be at most m * 2^k. Therefore, the overall time complexity is O(m * n * 2^k).

Space Complexity

O(R * C * 2^K) – The primary space usage comes from the queue used in the breadth-first search (BFS) and the visited set. The queue stores states, each consisting of a row, a column, and the keys collected so far. With R rows, C columns, and K keys, there are 2^K possible key combinations. The visited set stores the same kind of states, preventing revisits. Therefore, the space complexity is proportional to the number of possible states, which is R * C * 2^K, where R is the number of rows, C is the number of columns, and K is the number of keys. Thus, the auxiliary space complexity is O(R * C * 2^K).

Edge Cases

Case	How to Handle
Empty grid	Return -1 immediately since there's no path.
Grid with no keys or locks	Return 0 immediately since the starting point is the solution.
Starting point blocked by a wall	Return -1 as no path can be initiated.
No path exists to collect all keys	Return -1 if the BFS queue empties before all keys are collected.
Maximum grid size (30x30) with many keys	BFS might consume significant memory; ensure the solution doesn't exceed memory limits.
The starting point is adjacent to all the locks, but far away from keys	The algorithm must handle the correct order of getting keys before reaching locks.
Grid contains a cycle that must be traversed to get to a key	The visited set in BFS handles cycles effectively by avoiding revisiting states.
Key-lock pairs are not matched; a key opens a lock of a different letter	The problem assumes matching key-lock pairs based on letter case; solution will only work with matching pairs, return -1 if no solution exists