Smallest String Starting From Leaf
MediumYou are given the root of a binary tree where each node has a value in the range [0, 25] representing the letters 'a' to 'z'.
Return the lexicographically smallest string that starts at a leaf of this tree and ends at the root.
As a reminder, any shorter prefix of a string is lexicographically smaller.
- For example,
"ab"is lexicographically smaller than"aba".
A leaf of a node is a node that has no children.
Example 1:
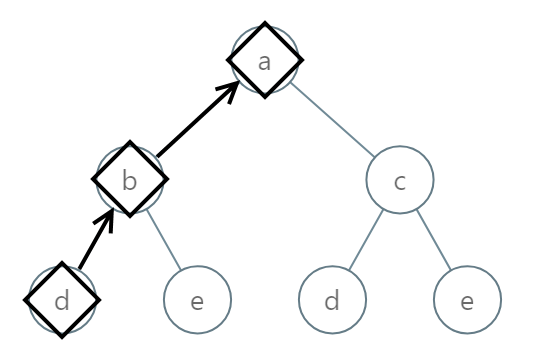
Input: root = [0,1,2,3,4,3,4] Output: "dba"
Example 2:
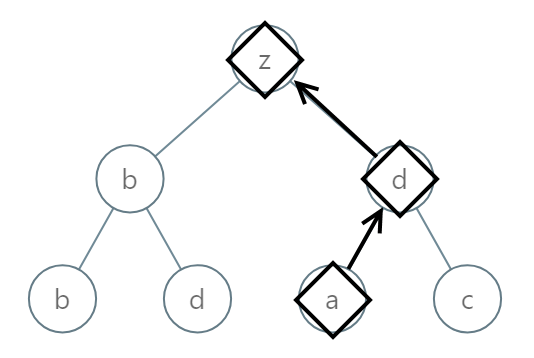
Input: root = [25,1,3,1,3,0,2] Output: "adz"
Example 3:

Input: root = [2,2,1,null,1,0,null,0] Output: "abc"
Constraints:
- The number of nodes in the tree is in the range
[1, 8500]. 0 <= Node.val <= 25
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What is the structure of the tree? Is it guaranteed to be a binary tree, or could it be a more general tree?
- What are the possible values for `node.val`? Are they limited to lowercase letters as suggested by the name, or can they be other characters or numbers?
- If there are multiple smallest strings, is any one of them acceptable, or is there a specific tie-breaking rule?
- Can the tree be empty? If so, what should the function return?
- Are there any limitations on the depth or number of nodes in the tree that might impact memory usage or algorithm choice?
Brute Force Solution
Approach
We want to find the smallest word you can spell out by walking from the bottom of a tree up to the top. The brute force method will try *every* possible path from each leaf all the way up to the root, forming a word for each path.
Here's how the algorithm would work step-by-step:
- Start at one of the leaf nodes (the bottom of the tree).
- Build a word by going up the tree, one node at a time, adding the letter for that node to the beginning of the word.
- Once you reach the very top (the root), you have one complete word.
- Remember this word.
- Now, repeat the process starting from a different leaf node. Build another word by going up the tree.
- Keep doing this for *every single* leaf node in the tree.
- After you've tried every possible path and have a collection of words, compare them all.
- The smallest word (alphabetically) is your answer.
Code Implementation
def smallest_from_leaf(root):
all_paths = []
def dfs(node, current_path):
if not node:
return
current_path = chr(node.val + ord('a')) + current_path
#If leaf node, add path to list
if not node.left and not node.right:
all_paths.append(current_path)
return
dfs(node.left, current_path)
dfs(node.right, current_path)
dfs(root, "")
#Need to handle the case when there's no root.
if not all_paths:
return ""
# Find lexographically smallest string.
smallest_string = all_paths[0]
for path in all_paths:
if path < smallest_string:
smallest_string = path
return smallest_stringBig(O) Analysis
Optimal Solution
Approach
The problem asks us to find the lexicographically smallest string formed by traversing from a leaf node to the root in a tree where each node represents a letter. We want to explore all paths from leaves to the root, converting each path into a string, and then finding the smallest string among them. We can use a depth-first search (DFS) approach to traverse the tree.
Here's how the algorithm would work step-by-step:
- Start a journey from each leaf node, working our way upwards toward the root node.
- As we travel up, collect the letters encountered along the path.
- Since we need the path from leaf to root, build the string by adding new letters to the beginning of our string, not the end.
- Once we reach the root from a leaf, we have a complete string representing a path.
- Compare the string we just created with the smallest string we've found so far. If the new string is smaller, remember it.
- Repeat this process for every leaf node in the tree.
- After checking all paths, the string we've remembered is the smallest string starting from a leaf.
Code Implementation
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
def smallest_from_leaf(root):
smallest_string = "~"
def depth_first_search(node, current_string):
nonlocal smallest_string
if not node:
return
current_string = chr(node.val + ord('a')) + current_string
# If it's a leaf node, compare and update the smallest string.
if not node.left and not node.right:
if current_string < smallest_string:
smallest_string = current_string
return
depth_first_search(node.left, current_string)
# Traverse right subtree only if it exists
depth_first_search(node.right, current_string)
# Initialize dfs from root with empty string
depth_first_search(root, "")
return smallest_stringBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Null or empty tree | Return an empty string if the root is null or the tree is empty. |
| Single node tree | Return the character corresponding to the single node's value. |
| Tree with only one path from root to leaf | The algorithm should still correctly construct the string from this path. |
| Deeply unbalanced tree (e.g., linked list structure) | Consider stack overflow issues with recursion and potentially use iterative approach if needed. |
| Tree with large number of nodes | The algorithm's space complexity must be considered for large trees, especially the string building and storage. |
| Multiple paths resulting in the same smallest string | The algorithm should return *any* of these smallest strings, fulfilling problem requirements. |
| Node values outside the range 0-25 | Throw an IllegalArgumentException or handle it according to the problem's constraints (if explicitly defined). |
| Tree contains duplicate paths leading to different strings | The algorithm should correctly compare and determine the smallest string among different paths. |