Snakes and Ladders #15 Most Asked
MediumYou are given an n x n integer matrix board where the cells are labeled from 1 to n2 in a Boustrophedon style starting from the bottom left of the board (i.e. board[n - 1][0]) and alternating direction each row.
You start on square 1 of the board. In each move, starting from square curr, do the following:
- Choose a destination square
nextwith a label in the range[curr + 1, min(curr + 6, n2)].- This choice simulates the result of a standard 6-sided die roll: i.e., there are always at most 6 destinations, regardless of the size of the board.
- If
nexthas a snake or ladder, you must move to the destination of that snake or ladder. Otherwise, you move tonext. - The game ends when you reach the square
n2.
A board square on row r and column c has a snake or ladder if board[r][c] != -1. The destination of that snake or ladder is board[r][c]. Squares 1 and n2 are not the starting points of any snake or ladder.
Note that you only take a snake or ladder at most once per dice roll. If the destination to a snake or ladder is the start of another snake or ladder, you do not follow the subsequent snake or ladder.
- For example, suppose the board is
[[-1,4],[-1,3]], and on the first move, your destination square is2. You follow the ladder to square3, but do not follow the subsequent ladder to4.
Return the least number of dice rolls required to reach the square n2. If it is not possible to reach the square, return -1.
Example 1:
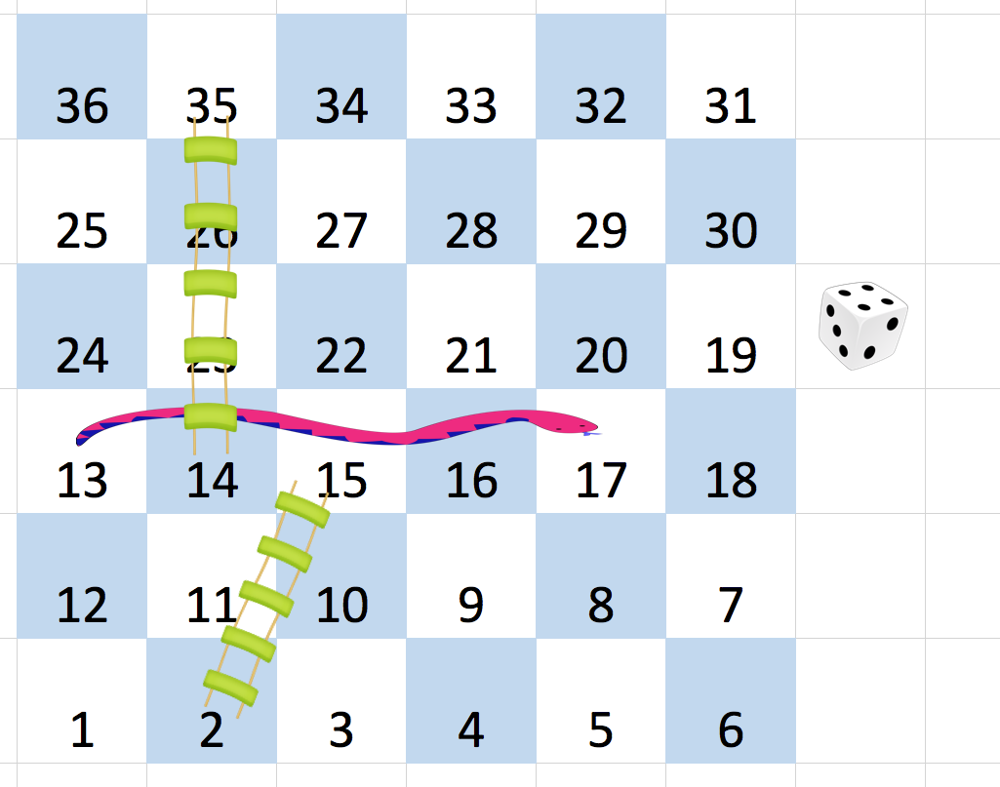
Input: board = [[-1,-1,-1,-1,-1,-1],[-1,-1,-1,-1,-1,-1],[-1,-1,-1,-1,-1,-1],[-1,35,-1,-1,13,-1],[-1,-1,-1,-1,-1,-1],[-1,15,-1,-1,-1,-1]] Output: 4 Explanation: In the beginning, you start at square 1 (at row 5, column 0). You decide to move to square 2 and must take the ladder to square 15. You then decide to move to square 17 and must take the snake to square 13. You then decide to move to square 14 and must take the ladder to square 35. You then decide to move to square 36, ending the game. This is the lowest possible number of moves to reach the last square, so return 4.
Example 2:
Input: board = [[-1,-1],[-1,3]] Output: 1
Constraints:
n == board.length == board[i].length2 <= n <= 20board[i][j]is either-1or in the range[1, n2].- The squares labeled
1andn2are not the starting points of any snake or ladder.
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What are the dimensions of the board (N x N), and what is the range of values for N?
- How are snakes and ladders represented? Specifically, if a cell contains a snake or ladder, what value will be stored there, and how does it map to the destination cell?
- Is it possible for a snake or ladder to start or end on the first or last cell (cell 1 or cell N*N)?
- If it's impossible to reach the end, what value should I return?
- Are there any negative cycles possible within the snake and ladder configurations (e.g., a snake leads to a ladder which leads back to the snake's starting point)? If so, how should I handle them?
Brute Force Solution
Approach
The brute force approach to Snakes and Ladders involves exploring every possible path a player can take on the board. We will simulate every possible sequence of dice rolls and moves until we find the shortest path to the end. It's like trying out every single option to guarantee finding the solution.
Here's how the algorithm would work step-by-step:
- Start at square one.
- Consider all six possible dice rolls (1 through 6).
- For each possible roll, move your piece accordingly, taking into account any snakes or ladders you land on.
- Repeat steps two and three for each new square you land on, considering all possible subsequent dice rolls from that square.
- Keep track of every possible sequence of moves and how many dice rolls it took to reach that square.
- Continue exploring paths until you reach the final square.
- Compare all the sequences of moves that led to the final square.
- Choose the sequence that used the fewest dice rolls; this is the shortest path.
Code Implementation
def snakes_and_ladders_brute_force(board, number_of_rows, number_of_columns):
board_size = number_of_rows * number_of_columns
queue = [(1, 0)]
visited = {1}
while queue:
current_square, moves = queue.pop(0)
if current_square == board_size:
return moves
# Consider all possible dice rolls (1 through 6).
for dice_roll in range(1, 7):
next_square = current_square + dice_roll
if next_square <= board_size:
# Account for snakes and ladders
row = (next_square - 1) // number_of_columns
col = (next_square - 1) % number_of_columns
if number_of_rows % 2 == 0:
if row % 2 == 0:
board_index = next_square - 1
else:
board_index = (row + 1) * number_of_columns - col - 1
else:
if row % 2 == 0:
board_index = (row + 1) * number_of_columns - col - 1
else:
board_index = next_square - 1
if board[number_of_rows - 1 - (board_index // number_of_columns)][board_index % number_of_columns] != -1:
next_square = board[number_of_rows - 1 - (board_index // number_of_columns)][board_index % number_of_columns]
# Only explore unvisited squares.
if next_square not in visited:
visited.add(next_square)
queue.append((next_square, moves + 1))
# If no path is found, return -1.
return -1Big(O) Analysis
Optimal Solution
Approach
The goal is to find the shortest path to the end of the board. We can treat the board as a graph and use a common graph search algorithm to find the quickest route.
Here's how the algorithm would work step-by-step:
- Think of each square on the board as a place you can be, and moving from one square to another as a step you can take.
- Imagine each square is connected to the next six squares (representing a die roll). If there's a snake or ladder, the connection goes to the square at the end of it instead.
- Start at the first square. Use a method that explores possible moves, like a breadth-first search. This helps you discover all reachable squares step-by-step.
- Keep track of how many dice rolls it takes to reach each square. That way, when you reach the final square, you'll know the smallest number of rolls it took.
- When you find a snake or ladder, immediately jump to the square it takes you to, and continue counting from there.
- Continue this process until you reach the final square. The number of rolls it took is the answer. If you explore every possible path without reaching the final square, then it is not possible to win the game.
Code Implementation
from collections import deque
def snakes_and_ladders(board):
board_size = len(board)
squares = board_size * board_size
def get_coordinates(square_number):
row = (square_number - 1) // board_size
col = (square_number - 1) % board_size
row = board_size - 1 - row
if (board_size % 2 == 0 and (board_size - 1 - row) % 2 != 0) or \
(board_size % 2 != 0 and (board_size - 1 - row) % 2 == 0):
col = board_size - 1 - col
return row, col
queue = deque([(1, 0)])
visited = {1}
while queue:
current_square, moves_made = queue.popleft()
if current_square == squares:
return moves_made
for dice_roll in range(1, 7):
next_square = current_square + dice_roll
if next_square > squares:
continue
row, col = get_coordinates(next_square)
# Account for snakes and ladders
if board[row][col] != -1:
next_square = board[row][col]
if next_square not in visited:
visited.add(next_square)
# Breadth-first search guarantees shortest path
queue.append((next_square, moves_made + 1))
return -1Big(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Null or empty board | Return -1 immediately as no game can be played. |
| Board size of 1x1 | Return 0 immediately since the start is already the end. |
| No ladders or snakes on the board | The shortest path will be the number of cells minus 1, proceed with standard BFS. |
| Start and end are directly connected by a ladder or snake | The BFS algorithm will prioritize this direct connection. |
| Board filled entirely with snakes leading to the start | The algorithm should correctly determine that the end cannot be reached and return -1. |
| Cyclic snakes and ladders leading nowhere | The visited set prevents infinite loops, allowing the algorithm to terminate if there's no path. |
| Integer overflow when calculating the next cell position | Use long data type to store cell positions before converting to row and column. |
| Maximum sized board (e.g., 20x20) | The BFS will still work, but the time and memory complexity may increase depending on the distribution of snakes and ladders; analyze for potential optimizations. |