Sort the Matrix Diagonally #6 Most Asked
MediumA matrix diagonal is a diagonal line of cells starting from some cell in either the topmost row or leftmost column and going in the bottom-right direction until reaching the matrix's end. For example, the matrix diagonal starting from mat[2][0], where mat is a 6 x 3 matrix, includes cells mat[2][0], mat[3][1], and mat[4][2].
Given an m x n matrix mat of integers, sort each matrix diagonal in ascending order and return the resulting matrix.
Example 1:
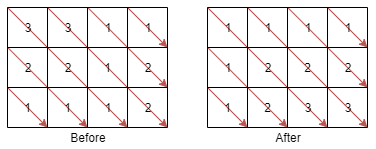
Input: mat = [[3,3,1,1],[2,2,1,2],[1,1,1,2]] Output: [[1,1,1,1],[1,2,2,2],[1,2,3,3]]
Example 2:
Input: mat = [[11,25,66,1,69,7],[23,55,17,45,15,52],[75,31,36,44,58,8],[22,27,33,25,68,4],[84,28,14,11,5,50]] Output: [[5,17,4,1,52,7],[11,11,25,45,8,69],[14,23,25,44,58,15],[22,27,31,36,50,66],[84,28,75,33,55,68]]
Constraints:
m == mat.lengthn == mat[i].length1 <= m, n <= 1001 <= mat[i][j] <= 100
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What is the range of values within the matrix, and can the matrix contain negative numbers or zeros?
- What should I return if the input matrix is null or empty?
- By 'diagonally', do you mean diagonals running from top-left to bottom-right, or should I consider both directions?
- Is it acceptable to modify the input matrix in place, or should I create a new matrix to return the result?
- What is the maximum size (number of rows and columns) of the input matrix?
Brute Force Solution
Approach
The brute force approach to sorting a matrix diagonally means we individually consider each diagonal. We extract the numbers on the diagonal, sort them, and then put the sorted numbers back into the original matrix.
Here's how the algorithm would work step-by-step:
- Start at the very top-left number of the matrix. This is the start of our first diagonal.
- Collect all the numbers along that diagonal in a separate list.
- Sort that list of numbers from smallest to largest.
- Put the sorted numbers back into the matrix, going along the same diagonal we took them from, starting from the top.
- Move to the next possible diagonal, which starts one position to the right of where we started originally.
- Repeat the process of extracting the numbers, sorting them, and putting them back, for this new diagonal.
- Keep doing this, moving one position to the right each time, until you reach the far right side.
- Once you are on the far right side, start back at the top-left position. Move one position down. Now you have the start of a new diagonal.
- Repeat the process of extracting the numbers, sorting them, and putting them back, for this new diagonal.
- Keep doing this, moving one position down each time, until you have covered every possible diagonal in the matrix.
- At the end, all the diagonals in the matrix will be sorted.
Code Implementation
def sort_the_matrix_diagonally(matrix):
number_of_rows = len(matrix)
number_of_columns = len(matrix[0])
# Iterate through the first row to start diagonals
for column_start_index in range(number_of_columns):
diagonal_values = []
row_index = 0
column_index = column_start_index
# Extract diagonal values
while row_index < number_of_rows and column_index < number_of_columns:
diagonal_values.append(matrix[row_index][column_index])
row_index += 1
column_index += 1
# Sort the diagonal values
diagonal_values.sort()
row_index = 0
column_index = column_start_index
sorted_index = 0
# Place sorted values back into the matrix
while row_index < number_of_rows and column_index < number_of_columns:
matrix[row_index][column_index] = diagonal_values[sorted_index]
row_index += 1
column_index += 1
sorted_index += 1
# Iterate through the first column to start diagonals
for row_start_index in range(1, number_of_rows):
diagonal_values = []
row_index = row_start_index
column_index = 0
# Extract diagonal values
while row_index < number_of_rows and column_index < number_of_columns:
diagonal_values.append(matrix[row_index][column_index])
row_index += 1
column_index += 1
# Sort the diagonal values
diagonal_values.sort()
row_index = row_start_index
column_index = 0
sorted_index = 0
# Place sorted values back into the matrix
while row_index < number_of_rows and column_index < number_of_columns:
# Filling back the sorted array
matrix[row_index][column_index] = diagonal_values[sorted_index]
row_index += 1
column_index += 1
sorted_index += 1
return matrixBig(O) Analysis
Optimal Solution
Approach
The key is to realize that all elements on the same diagonal have a consistent relationship between their row and column numbers. We can use this relationship to group the diagonal elements, sort them, and then place them back into the matrix.
Here's how the algorithm would work step-by-step:
- First, we need to identify all the diagonals in the matrix. A diagonal is defined by the fact that the difference between the row and column of any element in that diagonal is constant.
- Next, for each diagonal, we gather all its elements and put them into a temporary holding area.
- Then, we sort the numbers in the holding area for that specific diagonal from smallest to largest.
- Finally, we take the sorted numbers from the holding area and place them back into their original positions in the matrix, following the same diagonal path we extracted them from.
Code Implementation
def sort_the_matrix_diagonally(matrix):
number_of_rows = len(matrix)
number_of_columns = len(matrix[0])
# Iterate through the diagonals.
diagonals = {}
for row_index in range(number_of_rows):
for column_index in range(number_of_columns):
diagonal_index = row_index - column_index
# Group elements by their diagonal index.
if diagonal_index not in diagonals:
diagonals[diagonal_index] = []
diagonals[diagonal_index].append(matrix[row_index][column_index])
# Sort each diagonal.
for diagonal_index in diagonals:
diagonals[diagonal_index].sort()
# Place the sorted elements back.
for row_index in range(number_of_rows):
for column_index in range(number_of_columns):
diagonal_index = row_index - column_index
# Retrieve and place sorted values.
matrix[row_index][column_index] = diagonals[diagonal_index][0]
diagonals[diagonal_index].pop(0)
return matrixBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Null or empty matrix | Return the original null or empty matrix as there is nothing to sort. |
| 1x1 matrix | Return the original matrix as it is already diagonally sorted. |
| Matrix with only one row or one column | The algorithm should correctly handle single row/column matrices, essentially sorting the single row or column if the diagonal sorting is applied to the entire row or column, or return the original if diagonals shorter than two elements are not sorted. |
| Large matrix (e.g., 1000x1000) | Ensure the solution's time complexity is efficient enough to handle large matrices without exceeding time limits (ideally O(M*N*log(min(M,N)))). |
| Matrix with all identical values | The sorting algorithm should still function correctly and produce the same matrix as output because all the diagonals are already 'sorted'. |
| Matrix with negative and positive numbers | The sorting algorithm should handle both negative and positive integers without any issues using a general-purpose sorting algorithm. |
| Matrix with duplicate values within the same diagonal | The sorting algorithm should sort the diagonal including the duplicate values within that diagonal correctly. |
| Integer overflow during sorting or calculations | Use appropriate data types (e.g., long) or consider modular arithmetic if calculations could lead to integer overflow, particularly when determining diagonal indices. |