Special Positions in a Binary Matrix
Special Positions in a Binary Matrix #1 Most Asked
EasyGiven an m x n binary matrix mat, return the number of special positions in mat.
A position (i, j) is called special if mat[i][j] == 1 and all other elements in row i and column j are 0 (rows and columns are 0-indexed).
Example 1:
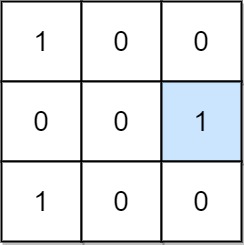
Input: mat = [[1,0,0],[0,0,1],[1,0,0]] Output: 1 Explanation: (1, 2) is a special position because mat[1][2] == 1 and all other elements in row 1 and column 2 are 0.
Example 2:
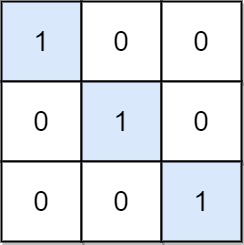
Input: mat = [[1,0,0],[0,1,0],[0,0,1]] Output: 3 Explanation: (0, 0), (1, 1) and (2, 2) are special positions.
Constraints:
m == mat.lengthn == mat[i].length1 <= m, n <= 100mat[i][j]is either0or1.
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What are the dimensions of the matrix? What are the upper bounds on the number of rows and columns?
- What values can the cells in the matrix hold? Are they restricted to 0 and 1, or can they be other integers?
- If no 'special' positions exist in the matrix, what should the function return?
- Is the input matrix guaranteed to be rectangular (i.e., all rows have the same number of columns)?
- By 'special position', do you mean that the element is the only 1 in its row and in its column simultaneously?
Brute Force Solution
Approach
The brute force method for finding special positions in a grid involves checking every position one by one. For each position, we examine its row and its column to see if it meets the special criteria. If it does, we count it; otherwise, we move on to the next position.
Here's how the algorithm would work step-by-step:
- Start by looking at the very first position in the grid.
- Check if the number in that position is a '1'. If it's not a '1', skip this position and go to the next one.
- If the number is a '1', check if there are any other '1's in the same row as this position.
- If there are other '1's in the same row, this position is not special, so move on to the next position in the grid.
- If there are no other '1's in the same row, check if there are any other '1's in the same column as this position.
- If there are other '1's in the same column, this position is also not special, so move on.
- If there are no other '1's in the same row or column, then this position is special, so increase the special position counter.
- Move to the next position in the grid and repeat steps 2 through 7 until you have checked every position in the grid.
- The final count of special positions is the answer.
Code Implementation
def special_positions_brute_force(matrix):
number_of_rows = len(matrix)
number_of_columns = len(matrix[0]) if number_of_rows > 0 else 0
special_position_count = 0
for row_index in range(number_of_rows):
for column_index in range(number_of_columns):
if matrix[row_index][column_index] == 1:
# Check for other 1s in the same row
is_special = True
for column_to_check in range(number_of_columns):
if column_to_check != column_index and matrix[row_index][column_to_check] == 1:
is_special = False
break
if is_special:
# Check for other 1s in the same column
for row_to_check in range(number_of_rows):
if row_to_check != row_index and matrix[row_to_check][column_index] == 1:
is_special = False
break
if is_special:
# Increment special position count if no other 1s
special_position_count += 1
return special_position_countBig(O) Analysis
Optimal Solution
Approach
The problem asks us to find special positions in a grid of zeros and ones. A position is special if its value is one, and that one is the only one in its row and column. Instead of checking every possible position, we can make it faster by focusing on rows and columns.
Here's how the algorithm would work step-by-step:
- First, for each row, count how many ones there are.
- Then, for each column, count how many ones there are.
- Now, go through each position in the grid.
- If a position has a one, check if its row has only one one and its column also has only one one.
- If both the row and column have only one one, then it's a special position, so increase the count.
- After checking every position, return the total count of special positions.
Code Implementation
def special_positions(matrix):
row_count = len(matrix)
column_count = len(matrix[0]) if row_count > 0 else 0
row_ones_count = [0] * row_count
column_ones_count = [0] * column_count
# Count ones in each row
for row_index in range(row_count):
for column_index in range(column_count):
if matrix[row_index][column_index] == 1:
row_ones_count[row_index] += 1
# Count ones in each column
for column_index in range(column_count):
for row_index in range(row_count):
if matrix[row_index][column_index] == 1:
column_ones_count[column_index] += 1
special_positions_count = 0
# Check each position for special condition
for row_index in range(row_count):
for column_index in range(column_count):
# Only check if the position has a 1
if matrix[row_index][column_index] == 1:
# Verify if it's the only 1 in its row and column.
if row_ones_count[row_index] == 1 and column_ones_count[column_index] == 1:
special_positions_count += 1
return special_positions_countBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Null or empty matrix | Return 0 immediately as there are no positions to check. |
| Matrix with 1 row or 1 column | Iterate through the single row/column and return the number of 1s if each '1' is the only '1' in its column/row. |
| Matrix filled with all 0s | Return 0 as no position can be special. |
| Matrix filled with all 1s | Return 0 as no position can be special because each row/column contains more than one '1'. |
| Very large matrix (e.g., 300x300) | The solution's time complexity should be O(m*n) where m and n are the dimensions, so ensure it can handle this size without timing out. |
| Rows or columns with multiple 1s | Ensure the code correctly identifies and excludes positions where a row or column has more than one '1'. |
| No special positions exist | The solution should correctly return 0 if no position satisfies the special condition. |
| Integer overflow when summing | Since the matrix values are either 0 or 1, and we are simply counting, integer overflow is not a concern here. |