Split the Array to Make Coprime Products

Hard

Zomato

10 views

Topics:

ArraysGreedy Algorithms

You are given a 0-indexed integer array nums of length n.

A split at an index i where 0 <= i <= n - 2 is called valid if the product of the first i + 1 elements and the product of the remaining elements are coprime.

For example, if nums = [2, 3, 3], then a split at the index i = 0 is valid because 2 and 9 are coprime, while a split at the index i = 1 is not valid because 6 and 3 are not coprime. A split at the index i = 2 is not valid because i == n - 1.

Return the smallest index i at which the array can be split validly or -1 if there is no such split.

Two values val1 and val2 are coprime if gcd(val1, val2) == 1 where gcd(val1, val2) is the greatest common divisor of val1 and val2.

Example 1:

Input: nums = [4,7,8,15,3,5]
Output: 2
Explanation: The table above shows the values of the product of the first i + 1 elements, the remaining elements, and their gcd at each index i.
The only valid split is at index 2.

Example 2:

Input: nums = [4,7,15,8,3,5]
Output: -1
Explanation: The table above shows the values of the product of the first i + 1 elements, the remaining elements, and their gcd at each index i.
There is no valid split.

Constraints:

n == nums.length
1 <= n <= 10⁴
1 <= nums[i] <= 10⁶

Try coding it in LeetCode

Split the Array to Make Coprime Products

Hard

Zomato

10 views

Topics:

ArraysGreedy Algorithms

You are given a 0-indexed integer array nums of length n.

A split at an index i where 0 <= i <= n - 2 is called valid if the product of the first i + 1 elements and the product of the remaining elements are coprime.

For example, if nums = [2, 3, 3], then a split at the index i = 0 is valid because 2 and 9 are coprime, while a split at the index i = 1 is not valid because 6 and 3 are not coprime. A split at the index i = 2 is not valid because i == n - 1.

Return the smallest index i at which the array can be split validly or -1 if there is no such split.

Two values val1 and val2 are coprime if gcd(val1, val2) == 1 where gcd(val1, val2) is the greatest common divisor of val1 and val2.

Example 1:

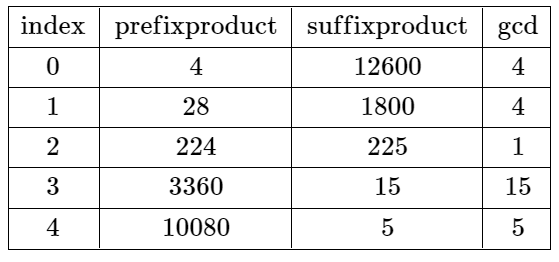
Input: nums = [4,7,8,15,3,5]
Output: 2
Explanation: The table above shows the values of the product of the first i + 1 elements, the remaining elements, and their gcd at each index i.
The only valid split is at index 2.

Example 2:

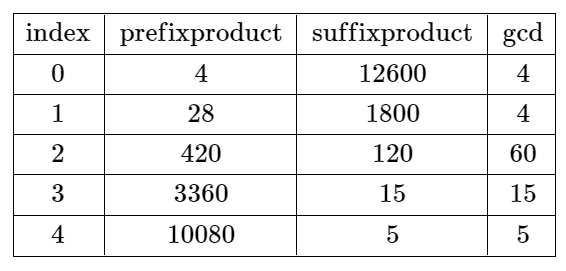
Input: nums = [4,7,15,8,3,5]
Output: -1
Explanation: The table above shows the values of the product of the first i + 1 elements, the remaining elements, and their gcd at each index i.
There is no valid split.

Constraints:

n == nums.length
1 <= n <= 10⁴
1 <= nums[i] <= 10⁶

Try coding it in LeetCode

Solution

Clarifying Questions

When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:

What is the maximum size of the input array `nums` and the range of values for each number in `nums`?
Can the input array `nums` contain duplicate numbers, and if so, how should they be handled?
If multiple split indices satisfy the coprime condition, which index should I return (e.g., the smallest, the largest)?
Is the input array guaranteed to have at least two elements?
Could you define 'coprime' explicitly, specifically, does it mean that the two products share no common factors other than 1?

Brute Force Solution

Approach

The brute force method for this question involves checking every possible way to split the given list of numbers into two groups. We want to find a split where the product of the numbers in each group has no common factors. This means trying absolutely every possible combination.

Here's how the algorithm would work step-by-step:

First, consider splitting the list so that the first group has only the first number.
Then, make the first group bigger by including the first two numbers, and check that possibility.
Continue making the first group larger, one number at a time, until it contains all but the last number.
For each of these possible splits, calculate the product of all the numbers in the first group.
Also, calculate the product of all the numbers in the second group.
Finally, check if these two products have any factors in common. If they don't, then this split works, and we can stop.
If none of the splits work where the first group is from one to all-but-one numbers, then there is no solution.

Code Implementation

def split_array_coprime_brute_force(numbers):
    list_length = len(numbers)

    for split_index in range(1, list_length): 
        # Iterate through all possible split points.

        first_group_product = 1
        for i in range(split_index):
            first_group_product *= numbers[i]

        second_group_product = 1
        for i in range(split_index, list_length):
            second_group_product *= numbers[i]

        # Check if products are coprime using GCD.
        if gcd(first_group_product, second_group_product) == 1:
            return True

    # If no split yielded coprime products, return false.
    return False

def gcd(first_number, second_number):
    #Euclidean Algorithm to find GCD.
    while(second_number):
        first_number, second_number = second_number, first_number % second_number

    return first_number

Big(O) Analysis

Time Complexity

O(n*a + n*b + n*gcd) – The brute force approach iterates through approximately n possible splits of the array. For each split, it calculates the product of the first group (which can take up to 'a' time if multiplication is considered O(a) where 'a' depends on bit size and number count for multiplication) and the product of the second group (similarly taking 'b' time). Finally, it computes the greatest common divisor (GCD) of these two products, which in the worst case takes O(gcd) time, where 'gcd' depends on the size of the products. Since these operations occur within the n loop, the total time complexity is O(n*a + n*b + n*gcd).

Space Complexity

O(1) – The provided brute force method calculates the product of two groups at each split. While the products themselves might grow very large, the algorithm doesn't explicitly store large intermediate data structures that scale with the input size N (where N is the number of elements in the input list). It only requires a constant number of variables to hold the current product of each group and potentially some counters or temporary variables for the multiplication, which do not depend on the size of the input array. Therefore, the space complexity is constant.

Optimal Solution

Approach

We need to find the best place to split a group of numbers so the resulting groups don't share any prime factors. Instead of trying all possible splits, we can efficiently track the prime factors we've seen so far and find the earliest point where a split would work.

Here's how the algorithm would work step-by-step:

First, find all the prime numbers that divide each number in the original group.
Then, start from the left and keep track of all the different prime numbers you've encountered so far.
As you move from left to right, check if the next number introduces any new prime numbers that you haven't seen before.
At each position, check if the prime numbers on the left side are completely different from the prime numbers on the right side. You can do this by seeing if the prime numbers you are tracking are contained within the remaining numbers.
If the prime numbers are different on both sides, then this is a valid split. Find the earliest valid split in the original sequence.

Code Implementation

def split_array_coprime_products(numbers):
    def find_prime_factors(number):
        prime_factors = set()
        divisor = 2
        while divisor * divisor <= number:
            if number % divisor == 0:
                prime_factors.add(divisor)
                while number % divisor == 0:
                    number //= divisor
            divisor += 1
        if number > 1:
            prime_factors.add(number)
        return prime_factors

    all_prime_factors = [find_prime_factors(number) for number in numbers]
    left_prime_factors = set()

    # Iterate through the numbers to find the earliest split
    for i in range(len(numbers) - 1):
        left_prime_factors.update(all_prime_factors[i])

        right_prime_factors = set()
        for j in range(i + 1, len(numbers)):
            right_prime_factors.update(all_prime_factors[j])

        # Check for coprime condition between left and right sides.
        if not left_prime_factors.intersection(right_prime_factors):
            return i

    # No valid split found
    return -1

Big(O) Analysis

Time Complexity

O(n * m) – The algorithm iterates through each of the n numbers in the input array. For each number, it finds its prime factors. Assuming that the largest number in the array has m prime factors on average (or that the algorithm spends O(m) to find and store its prime factors), this operation is repeated for each of the n numbers. Therefore, the overall time complexity is approximately O(n * m).

Space Complexity

O(N + M) – The algorithm calculates prime factors for each number in the input array of size N. This could involve storing a list of prime factors for each number, potentially requiring O(N*M) space in the worst case where M is the number of prime factors for a single number in the input array. The algorithm also tracks the unique prime numbers encountered on the left side of the split, which could grow up to O(M), where M is the number of distinct prime factors across all numbers in the input array. Additionally, it implicitly needs to store a set of prime factors for the numbers on the right side to perform comparisons, but the maximum size of this set is bounded by the total number of primes, M. Combining, the space used is O(N + M) where N is the number of elements in the array and M is the total number of distinct prime factors across all numbers in the input array. Note that the prime factorization doesn't need to store N*M, it can store at most the maximum number of primes found in any of the N numbers. It is also important to remember that the problem wants us to find the EARLIEST split possible.

Edge Cases

Case	How to Handle
Empty or null input array	Return -1 immediately since no split is possible.
Input array with only one element	Return -1 since the subarrays must be non-empty.
All numbers in the array are 1	Return -1 as the product of any subarray will be 1, and thus coprime with the other.
All numbers in the array share a common prime factor	Return -1 because the products of any two subarrays will share that prime factor.
Large input array with large numbers, potential integer overflow when calculating products	Use a prime factorization approach to avoid explicitly calculating large products, working with prime factors instead.
Array contains numbers that are powers of the same prime (e.g., [2, 4, 8])	The prime factorization approach correctly identifies that any split will result in subarrays that share the prime factor.
Multiple valid split points exist	Iterate through the array from left to right and return the first valid split point encountered.
Input array contains very large prime numbers	Ensure the prime factorization algorithm can handle large numbers efficiently, possibly using precomputed primes or optimized algorithms.