Stamping the Grid
HardYou are given an m x n binary matrix grid where each cell is either 0 (empty) or 1 (occupied).
You are then given stamps of size stampHeight x stampWidth. We want to fit the stamps such that they follow the given restrictions and requirements:
- Cover all the empty cells.
- Do not cover any of the occupied cells.
- We can put as many stamps as we want.
- Stamps can overlap with each other.
- Stamps are not allowed to be rotated.
- Stamps must stay completely inside the grid.
Return true if it is possible to fit the stamps while following the given restrictions and requirements. Otherwise, return false.
Example 1:
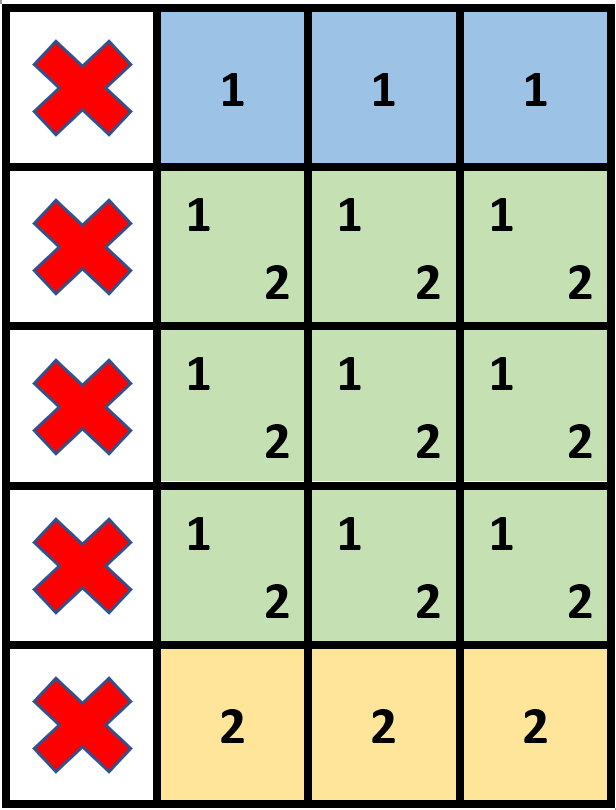
Input: grid = [[1,0,0,0],[1,0,0,0],[1,0,0,0],[1,0,0,0],[1,0,0,0]], stampHeight = 4, stampWidth = 3 Output: true Explanation: We have two overlapping stamps (labeled 1 and 2 in the image) that are able to cover all the empty cells.
Example 2:
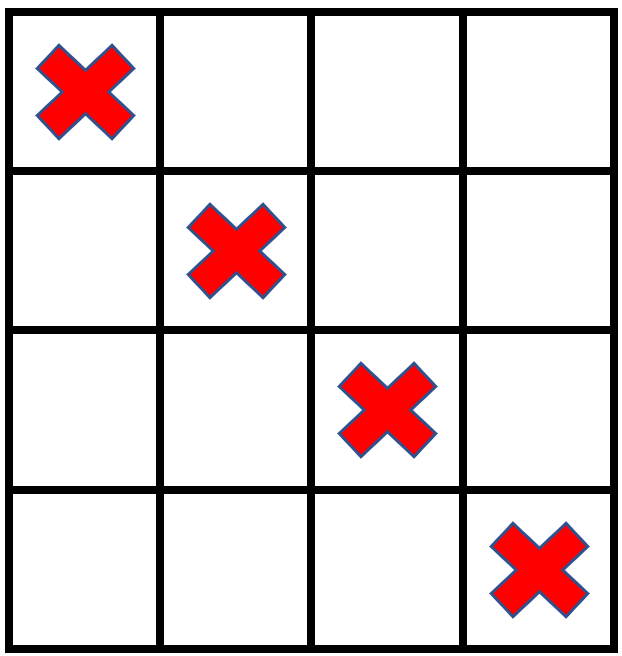
Input: grid = [[1,0,0,0],[0,1,0,0],[0,0,1,0],[0,0,0,1]], stampHeight = 2, stampWidth = 2 Output: false Explanation: There is no way to fit the stamps onto all the empty cells without the stamps going outside the grid.
Constraints:
m == grid.lengthn == grid[r].length1 <= m, n <= 1051 <= m * n <= 2 * 105grid[r][c]is either0or1.1 <= stampHeight, stampWidth <= 105
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What are the constraints on m, n, stampHeight, and stampWidth? Specifically, what are the maximum and minimum values?
- If it's impossible to cover all 0s with the stamp, should I return `false`, or is there a different value I should return in that case?
- Can the `grid` matrix be empty (m=0 or n=0), and what should I return in that scenario?
- Is `stampHeight` or `stampWidth` ever 0? If so, what is the expected behavior?
- If there are multiple valid ways to place the stamps, am I required to find a specific arrangement, or can I return `true` as soon as I find *any* valid arrangement?
Brute Force Solution
Approach
The brute force approach to solving this stamping problem involves trying all possible placements of the stamp on the grid. We systematically check every potential location and orientation to see if the stamping constraints are satisfied. If it works, it's a valid stamping, and we can record it.
Here's how the algorithm would work step-by-step:
- Consider the stamp. Imagine picking it up and placing it down on the grid.
- Start at the very top-left corner and try stamping it there. Check if it covers any forbidden areas or goes outside the grid.
- If the stamp placement is valid, remember that location. If not, forget about it.
- Move the stamp slightly to the right and repeat the checking process.
- Continue moving the stamp across the row, checking for validity at each spot.
- Once you reach the end of the row, move the stamp down one position and start again from the left.
- Keep doing this until you have tried stamping the grid at every possible position.
- After trying all placements, analyze the valid stamp locations to see if all the necessary areas are covered.
Code Implementation
def stamp_the_grid_brute_force(grid, stamp_height, stamp_width):
grid_height = len(grid)
grid_width = len(grid[0])
valid_stamps = []
for row_start in range(grid_height):
for col_start in range(grid_width):
# Check if the stamp placement is valid given the grid size
if row_start + stamp_height <= grid_height and col_start + stamp_width <= grid_width:
is_valid = True
for row in range(row_start, row_start + stamp_height):
for col in range(col_start, col_start + stamp_width):
# Check if stamping here would cover a forbidden area
if grid[row][col] == 1:
is_valid = False
break
if not is_valid:
break
if is_valid:
valid_stamps.append((row_start, col_start))
# After finding all valid stamp placements, check if entire grid is covered
if not valid_stamps:
return False
covered_grid = [[0] * grid_width for _ in range(grid_height)]
for row_start, col_start in valid_stamps:
for row in range(row_start, row_start + stamp_height):
for col in range(col_start, col_start + stamp_width):
covered_grid[row][col] = 1
for row in range(grid_height):
for col in range(grid_width):
# Verify all required areas are covered
if grid[row][col] == 0 and covered_grid[row][col] == 0:
return False
return TrueBig(O) Analysis
Optimal Solution
Approach
The trick is to avoid redundant checks by working backward and strategically filling in the grid. We start by figuring out where stamps *must* be placed and then checking if this arrangement satisfies the initial constraints. If it does, we're golden!
Here's how the algorithm would work step-by-step:
- First, let's identify all the cells that absolutely need to be covered by a stamp. These are the marked cells in our grid.
- Now, pretend we have placed stamps to cover all those necessary cells. Specifically, place them so their top-left corner touches each necessary cell.
- Next, imagine the resulting grid after all these stamps have been applied. Check if there are now any marked cells left uncovered. If there are, it's impossible, and we're done.
- After that, we need to check for the opposite problem: that we didn't accidentally stamp any empty cells. If we did, it's also impossible.
- Finally, if we made it this far, it means we successfully covered all the marked cells without stamping any empty ones, and we've found a solution.
Code Implementation
def stamping_the_grid(grid, stamp_height, stamp_width):
grid_height = len(grid)
grid_width = len(grid[0])
stamped_grid = [[0] * grid_width for _ in range(grid_height)]
# Mark cells that must be covered.
necessary_cells = []
for row in range(grid_height):
for col in range(grid_width):
if grid[row][col] == 1:
necessary_cells.append((row, col))
# Place stamps at each necessary cell.
for row, col in necessary_cells:
for stamp_row in range(stamp_height):
for stamp_col in range(stamp_width):
current_row = row + stamp_row
current_col = col + stamp_col
if 0 <= current_row < grid_height and 0 <= current_col < grid_width:
stamped_grid[current_row][current_col] = 1
# Check if any marked cells are now uncovered.
for row in range(grid_height):
for col in range(grid_width):
if grid[row][col] == 1 and stamped_grid[row][col] == 0:
return False
# Avoid stamping empty cells
for row in range(grid_height):
for col in range(grid_width):
if grid[row][col] == 0 and stamped_grid[row][col] == 1:
return False
return TrueBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Null or empty grid | Return true if grid is null or empty as there are no 0s to cover. |
| Stamp dimensions larger than grid dimensions | If stamp dimensions exceed grid, valid placement isn't possible unless the entire grid is 0, so check if all grid elements are 0. |
| Stamp dimensions are 1x1 | Check if all 0s in the grid can be covered with 1x1 stamps which is always possible if grid[i][j]==0. |
| Grid filled entirely with 1s | Return true, as there are no 0s to cover. |
| Grid filled entirely with 0s and stamp covers the entire grid | Return true if the stamp covers the entire grid, implying only one stamp placement is needed and valid. |
| Grid with single 0 surrounded by 1s, stamp larger than 1x1 | If the stamp is bigger than 1x1, and a single 0 is surrounded by 1's, it cannot be covered, return false. |
| Large grid dimensions (m, n are large) leading to potential memory issues | Optimize space complexity by using difference arrays to track overlapping stamp placements efficiently. |
| Integer overflow when calculating stamp positions or coverage area | Ensure that intermediate calculations like grid indices or stamp counts are within integer bounds to avoid unexpected results. |