Subtree of Another Tree
EasyGiven the roots of two binary trees root and subRoot, return true if there is a subtree of root with the same structure and node values of subRoot and false otherwise.
A subtree of a binary tree tree is a tree that consists of a node in tree and all of this node's descendants. The tree tree could also be considered as a subtree of itself.
Example 1:
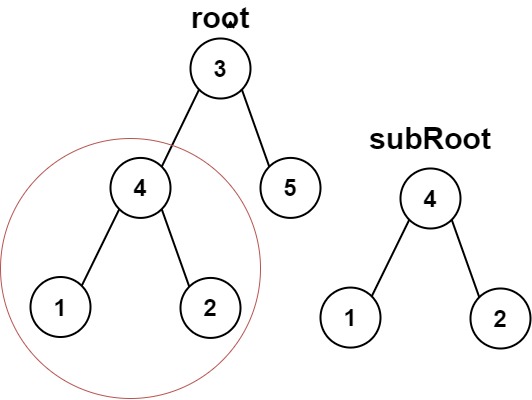
Input: root = [3,4,5,1,2], subRoot = [4,1,2] Output: true
Example 2:

Input: root = [3,4,5,1,2,null,null,null,null,0], subRoot = [4,1,2] Output: false
Constraints:
- The number of nodes in the
roottree is in the range[1, 2000]. - The number of nodes in the
subRoottree is in the range[1, 1000]. -104 <= root.val <= 104-104 <= subRoot.val <= 104
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- Are the node values guaranteed to be unique within each tree, or can duplicate values exist?
- What is the expected range of values for the nodes in the trees? Can they be null or negative?
- Can either `root` or `subRoot` be an empty tree (i.e., null)? If so, what should be returned?
- Does the definition of a subtree require that the structure exactly matches, or is it permissible for node values to be identical but the structural arrangement to differ?
- Are there any constraints on the height or number of nodes in the trees that might influence the choice of algorithm or data structures?
Brute Force Solution
Approach
To find if one tree is a part of another, we can imagine trying to place the smaller tree on top of the larger tree at every possible starting point. We then check if the arrangement perfectly matches.
Here's how the algorithm would work step-by-step:
- Start by looking at the very top of the larger tree.
- See if the smaller tree perfectly matches the larger tree starting from this top point.
- If it doesn't match, move down to the next possible starting point in the larger tree.
- Try matching the smaller tree again from this new starting point.
- Continue this process, moving to every single node in the larger tree as a potential starting point for the smaller tree.
- If at any point the smaller tree perfectly lines up with a part of the larger tree, we've found our answer.
- If we check every single possible starting point in the larger tree and none of them result in a perfect match, then the smaller tree is not a part of the larger tree.
Code Implementation
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
def are_identical(tree_node_s, tree_node_t):
if tree_node_s is None and tree_node_t is None:
return True
if tree_node_s is None or tree_node_t is None:
return False
if tree_node_s.val != tree_node_t.val:
return False
# Recursively check if the left and right subtrees are identical
return are_identical(tree_node_s.left, tree_node_t.left) and are_identical(tree_node_s.right, tree_node_t.right)
def is_subtree(tree_node_s, tree_node_t):
if tree_node_t is None:
return True
if tree_node_s is None:
return False
# First, check if the current nodes and their subtrees match exactly
if are_identical(tree_node_s, tree_node_t):
return True
# If not, we need to explore the left and right children of the larger tree
# This is to find a new potential starting point for the smaller tree
return is_subtree(tree_node_s.left, tree_node_t) or is_subtree(tree_node_s.right, tree_node_t)
Big(O) Analysis
Optimal Solution
Approach
The optimal strategy involves two main parts: first, checking if one tree is an exact copy of another starting from their roots, and second, systematically checking every possible starting point in the larger tree to see if a matching subtree exists.
Here's how the algorithm would work step-by-step:
- Imagine you have two tree-like structures. You want to know if one smaller tree is exactly present within a larger tree.
- The first step is to have a way to compare two trees and see if they are identical, branch for branch and value for value, starting from their very tops.
- Now, take the larger tree. You need to visit every single point within this larger tree.
- At each point you visit in the larger tree, pretend that point is the very top of a potential matching smaller tree.
- Use your comparison tool (from step two) to see if the structure starting from this current point in the larger tree perfectly matches the entire smaller tree.
- If you find even one point in the larger tree where the structure perfectly matches the smaller tree, then you've found your answer, and you can stop looking.
- If you go through every single point in the larger tree and none of them start a structure that matches the smaller tree, then the smaller tree is not a subtree of the larger one.
Code Implementation
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.node_value = val
self.left_child = left
self.right_child = right
def are_trees_identical(first_tree_root, second_tree_root):
# Base case: Both nodes are None, meaning they match.
if not first_tree_root and not second_tree_root:
return True
# Base case: One node is None and the other is not, they don't match.
if not first_tree_root or not second_tree_root:
return False
# Check if the current nodes have the same value and their subtrees are also identical.
return (first_tree_root.node_value == second_tree_root.node_value and
are_trees_identical(first_tree_root.left_child, second_tree_root.left_child) and
are_trees_identical(first_tree_root.right_child, second_tree_root.right_child))
def is_subtree(larger_tree_root, smaller_tree_root):
# If the smaller tree is empty, it's considered a subtree of any tree.
if not smaller_tree_root:
return True
# If the larger tree is empty but the smaller one isn't, it cannot be a subtree.
if not larger_tree_root:
return False
# Check if the subtree rooted at the current node in the larger tree matches the smaller tree.
if are_trees_identical(larger_tree_root, smaller_tree_root):
return True
# Recursively check if the smaller tree is a subtree of the left or right child of the larger tree.
return (is_subtree(larger_tree_root.left_child, smaller_tree_root) or
is_subtree(larger_tree_root.right_child, smaller_tree_root))Big(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Both root and subRoot are null | An empty tree is considered a subtree of another empty tree. |
| root is null but subRoot is not null | A non-empty tree cannot be a subtree of an empty tree. |
| subRoot is null but root is not null | An empty tree is considered a subtree of any non-empty tree. |
| root and subRoot are identical single-node trees | The algorithm should correctly identify the single node as matching. |
| subRoot is a single node and root is a much larger tree | The traversal should exhaustively search for the single node and its descendants. |
| root has many nodes but subRoot is deeply nested | The recursive comparison function must handle deep recursion without stack overflow issues for typical interview constraints. |
| root and subRoot have identical structures and values but are different instances | The comparison must be based on node values and structural integrity, not object identity. |
| subRoot's values appear multiple times in root, but not as a contiguous subtree | The algorithm must verify the entire structure of subRoot starting from a matching node in root, not just individual value matches. |