Sum Root to Leaf Numbers
Medium
1 view
Topics:
TreesRecursion
You are given the root of a binary tree containing digits from 0 to 9 only.
Each root-to-leaf path in the tree represents a number.
- For example, the root-to-leaf path
1 -> 2 -> 3represents the number123.
Return the total sum of all root-to-leaf numbers. Test cases are generated so that the answer will fit in a 32-bit integer.
A leaf node is a node with no children.
Example 1:
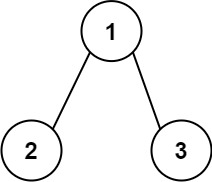
Input: root = [1,2,3] Output: 25 Explanation: The root-to-leaf path1->2represents the number12. The root-to-leaf path1->3represents the number13. Therefore, sum = 12 + 13 =25.
Example 2:
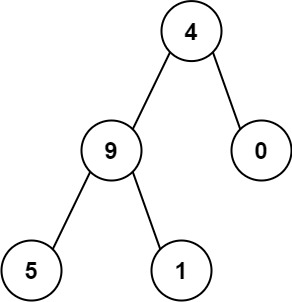
Input: root = [4,9,0,5,1] Output: 1026 Explanation: The root-to-leaf path4->9->5represents the number 495. The root-to-leaf path4->9->1represents the number 491. The root-to-leaf path4->0represents the number 40. Therefore, sum = 495 + 491 + 40 =1026.
Constraints:
- The number of nodes in the tree is in the range
[1, 1000]. 0 <= Node.val <= 9- The depth of the tree will not exceed
10.
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- Can the tree be empty, and if so, what should I return?
- Are the node values guaranteed to be single digits (0-9)?
- What is the maximum depth of the tree, and should I be concerned about potential stack overflow issues with recursion?
- If a node has only one child, is that still considered a root-to-leaf path?
- Could a node's value be zero, and if so, does that affect the overall number calculation?
Brute Force Solution
Approach
The problem asks us to find the sum of all numbers formed by paths from the root to the leaves in a tree. The brute force approach will explore every possible path from the root to a leaf, calculating the number for each path, and finally summing all those numbers together.
Here's how the algorithm would work step-by-step:
- Start at the very top of the tree, the root node.
- Imagine walking down the tree, exploring every possible path you can take from the root.
- At each step, you are building a number by adding the value of the current node to the number you've built so far.
- Whenever you reach a leaf (a node with no children), you've completed a path and formed a complete number.
- Remember this number and set it aside.
- Continue exploring all other possible paths from the root to other leaves.
- Once you've explored all paths and found all the numbers, add all the numbers you set aside together to get the final sum.
Code Implementation
def sum_root_to_leaf(root):
def dfs(node, current_number):
if not node:
return 0
current_number = current_number * 10 + node.val
# If we are at a leaf node, add the current number to the total
if not node.left and not node.right:
return current_number
# Recursively explore the left and right subtrees
return dfs(node.left, current_number) + dfs(node.right, current_number)
return dfs(root, 0)
Big(O) Analysis
Time Complexity
O(n) – The algorithm traverses a binary tree, visiting each node once. The number of nodes in the tree is represented by 'n'. Each node visit involves a constant amount of work to update the path number. Since every node is visited exactly once, the time complexity is directly proportional to the number of nodes. Therefore, the time complexity is O(n).
Space Complexity
O(H) – The algorithm explores all root-to-leaf paths, which can be implemented using recursion. The maximum depth of the recursive calls is determined by the height (H) of the tree, where each recursive call adds a new frame to the call stack. The auxiliary space used is primarily due to the call stack during recursion. In the worst-case scenario (a skewed tree), H can be equal to N (the number of nodes), and in the best-case scenario (a balanced tree), H is log(N). Thus, the space complexity is O(H), where H is the height of the tree.
Optimal Solution
Approach
The core idea is to traverse the tree in a way that builds the number from the root to each leaf as we go. We keep track of the number formed so far and update it as we move down the tree.
Here's how the algorithm would work step-by-step:
- Start at the very top of the tree, the root.
- Imagine you're building a number step-by-step as you walk down the tree.
- At each step, you add the current node's value to the number you've built so far, effectively extending it by one digit to the right.
- When you reach a leaf (a node with no children), the number you've built is a root-to-leaf number. Add this number to a running total.
- If you reach a node with one or two children, continue moving down the tree, passing the currently built number to each child to extend.
- Once you have explored every path from the root to every leaf, return the total sum of all the root-to-leaf numbers you found.
Code Implementation
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
def sum_numbers(root):
def dfs(node, current_number):
if not node:
return 0
current_number = current_number * 10 + node.val
# If it's a leaf, add the number to the total.
if not node.left and not node.right:
return current_number
# Explore the left and right subtrees.
left_sum = dfs(node.left, current_number)
right_sum = dfs(node.right, current_number)
# Summing up the paths from left and right
return left_sum + right_sum
# Initiate the depth-first search from the root.
return dfs(root, 0)
Big(O) Analysis
Time Complexity
O(n) – The algorithm visits each node in the binary tree exactly once. The amount of work done at each node (multiplying the existing path value by 10 and adding the node's value) is constant. Therefore, the time complexity is directly proportional to the number of nodes in the tree, which is n. Consequently, the time complexity is O(n).
Space Complexity
O(H) – The algorithm uses recursion to traverse the tree. The maximum depth of the recursion stack is equal to the height of the tree, denoted as H. In the worst-case scenario (a skewed tree), H can be equal to N, where N is the number of nodes in the tree. Therefore, the auxiliary space complexity is O(H), representing the space used by the call stack.
Edge Cases
| Case | How to Handle |
|---|---|
| Null root node | Return 0 immediately since there are no root-to-leaf paths. |
| Single node tree (root is also a leaf) | Return the value of the root node as it represents a single path. |
| Tree with all nodes having value 0 | The algorithm should correctly compute the sum of all root-to-leaf numbers, which will be 0. |
| Tree with very long paths leading to potential integer overflow | Use a data type that can handle larger numbers, or use modular arithmetic during path number construction. |
| Tree where all left children are null | The algorithm should still correctly traverse and sum the root-to-leaf paths even with a skewed tree structure. |
| Tree where all right children are null | The algorithm should still correctly traverse and sum the root-to-leaf paths even with a skewed tree structure. |
| Deeply unbalanced tree causing stack overflow in recursive solutions | Consider an iterative approach (e.g., using a stack) instead of recursion to avoid exceeding stack limits. |
| Nodes with non-digit values (outside 0-9 range) | Add validation to ensure nodes only contain digits and return an error or handle as 0 if invalid data is found. |
Explore Interview QuestionsGoogle Interview QuestionsMeta Interview QuestionsAmazon Interview QuestionsApple Interview QuestionsNetflix Interview Questions
Explore Jobs By LevelEntry-Level Software Engineer JobsMid-Level Software Engineer JobsSenior Software Engineer JobsStaff Software Engineer Jobs
