The Maze #12 Most Asked
MediumThere is a ball in a maze with empty spaces and walls. The ball can go through empty spaces by rolling up, down, left or right, but it won't stop rolling until hitting a wall. When the ball stops, it could choose the next direction.
Given the maze, the ball's start position and the destination, where maze[i][j] = 0 represents empty space and maze[i][j] = 1 represents the wall. Find whether the ball could stop at the destination.
The maze is represented by a binary 2D array. The start and destination coordinates are represented by row and column indexes.
Example 1:
Input 1: a maze represented by a 2D array
0 0 1 0 0
0 0 0 0 0
0 0 0 1 0
1 1 0 1 1
0 0 0 0 0
Input 2: start coordinate (rowStart, colStart) = (0, 4)
Input 3: destination coordinate (rowDest, colDest) = (4, 4)
Output: true
Explanation: One possible way is : left -> down -> left -> down -> right -> down -> right.
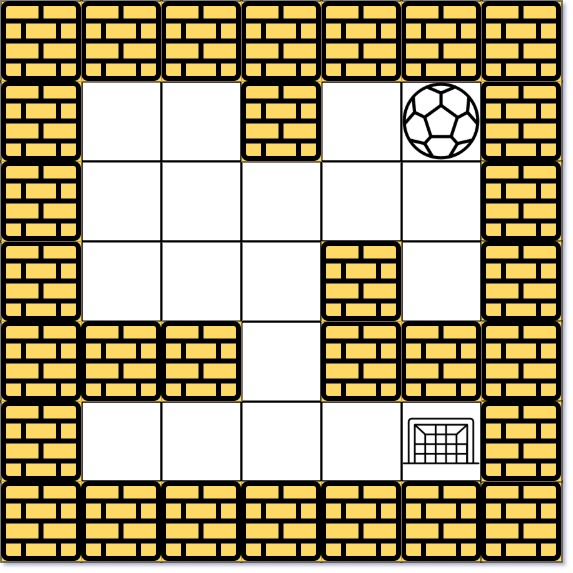
Example 2:
Input 1: a maze represented by a 2D array
0 0 1 0 0
0 0 0 0 0
0 0 0 1 0
1 1 0 1 1
0 0 0 0 0
Input 2: start coordinate (rowStart, colStart) = (0, 4)
Input 3: destination coordinate (rowDest, colDest) = (3, 2)
Output: false
Explanation: There is no way for the ball to stop at the destination.
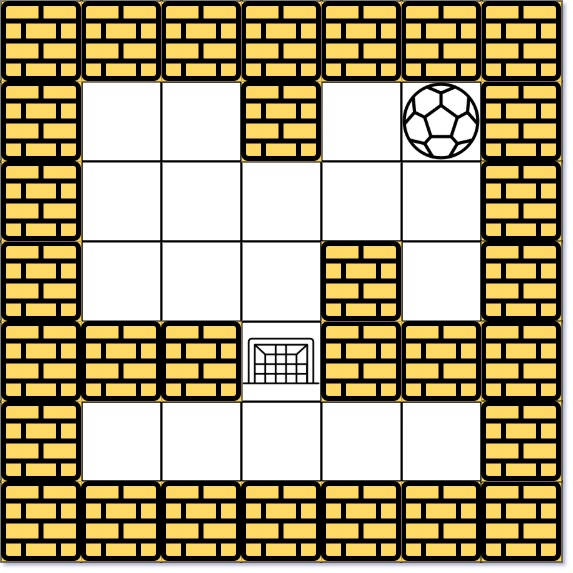
Constraints:
1 <= maze.length, maze[i].length <= 100maze[i][j]is0or1.0 <= rowStart, rowDest < maze.length0 <= colStart, colDest < maze[i].length- Both the ball and the destination exist on an empty space, and they will not be at the same position initially.
- The maze does not contain border (like the edge walls).
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What are the dimensions of the maze (maximum rows and columns)?
- Can the start and destination coordinates be outside the bounds of the maze?
- Is it guaranteed that the start and destination coordinates are valid (i.e., within the maze bounds and not walls)?
- If there are multiple shortest paths, is any one of them acceptable?
- Can we assume the maze will always be rectangular, or could it be an irregular shape?
Brute Force Solution
Approach
Think of solving a maze by trying every possible path. The brute force way means we explore each direction from our starting point until we find the exit, or we hit a dead end. If we hit a dead end, we backtrack and try a different direction.
Here's how the algorithm would work step-by-step:
- Start at the beginning of the maze.
- Try going forward, if possible.
- If you can't go forward, try turning right. If you can't turn right, try turning left. If you can't turn left, go back the way you came.
- Keep going until you reach the end of the maze.
- If you reach a dead end, go back to the last place where you had a choice and try a different path.
- Repeat this process of trying every possible path until you find the exit.
Code Implementation
def solve_maze_brute_force(maze, start, end):
path = [start]
visited = {start}
def find_path():
nonlocal path, visited
if path[-1] == end:
return path
row, col = path[-1]
# Possible movements: right, down, left, up
movements = [(0, 1), (1, 0), (0, -1), (-1, 0)]
for row_change, col_change in movements:
new_row, new_col = row + row_change, col + col_change
# Check for valid move
if (0 <= new_row < len(maze) and
0 <= new_col < len(maze[0]) and
maze[new_row][new_col] == 0 and
(new_row, new_col) not in visited):
# Mark current spot in the path as visited
visited.add((new_row, new_col))
path.append((new_row, new_col))
new_path = find_path()
if new_path:
return new_path
# Backtrack if path not found
path.pop()
visited.remove((new_row, new_col))
return None
return find_path()Big(O) Analysis
Optimal Solution
Approach
To find the shortest path through a maze, we'll use a method that explores the maze level by level. This guarantees that the first time we reach the destination, it will be by the shortest route. Think of it like ripples in a pond, expanding outward from the start.
Here's how the algorithm would work step-by-step:
- Start at the beginning of the maze.
- Imagine exploring all possible paths one step at a time, simultaneously.
- Keep track of how many steps it takes to reach each new spot in the maze.
- When you reach the end of the maze, the number of steps you took is the length of the shortest path.
- If you find the end by a certain path, you know it is the shortest path because you checked all shorter paths first.
Code Implementation
from collections import deque
def find_shortest_maze_path(maze, start, destination):
rows = len(maze)
cols = len(maze[0])
queue = deque([(start, 0)])
visited = {start}
# Possible movements: up, down, left, right.
possible_moves = [(0, 1), (0, -1), (1, 0), (-1, 0)]
while queue:
(row, col), steps = queue.popleft()
if (row, col) == destination:
return steps
# Explore all possible moves from current cell
for delta_row, delta_col in possible_moves:
new_row = row + delta_row
new_col = col + delta_col
# Check if the new position is valid.
if 0 <= new_row < rows and 0 <= new_col < cols and \
maze[new_row][new_col] == 0 and (new_row, new_col) not in visited:
# Add valid and unvisited neighbors to queue
queue.append(((new_row, new_col), steps + 1))
visited.add((new_row, new_col))
return -1 # No path found.Big(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Null or empty maze | Return -1 immediately as there is no maze to traverse. |
| Start or destination out of bounds | Return -1 if start or destination coordinates are outside maze dimensions. |
| Start equals destination | Return 0 because no movement is required to reach the destination. |
| Maze with only one cell and start equals destination | Return 0 if the maze is a single cell and the start and destination are that cell. |
| Maze completely blocked (all 1s), start != destination | Return -1 as the destination is unreachable. |
| Maze with no path to destination | Return -1 after exploring all possible paths without finding the destination. |
| Integer overflow in distance calculation with large mazes | Use a data type with a larger range (e.g., long) to store distances to prevent potential overflows. |
| Large maze causing excessive memory usage in BFS/DFS | Consider using iterative BFS with proper memory management to avoid stack overflow or excessive memory consumption. |