Tiling a Rectangle with the Fewest Squares
HardGiven a rectangle of size n x m, return the minimum number of integer-sided squares that tile the rectangle.
Example 1:
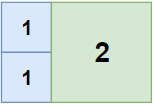
Input: n = 2, m = 3 Output: 3 Explanation:3squares are necessary to cover the rectangle.2(squares of1x1)1(square of2x2)
Example 2:
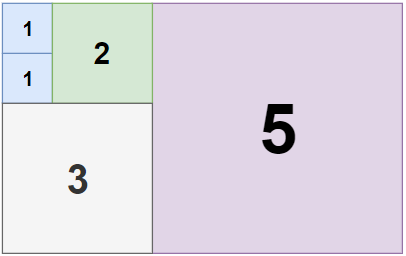
Input: n = 5, m = 8 Output: 5
Example 3:
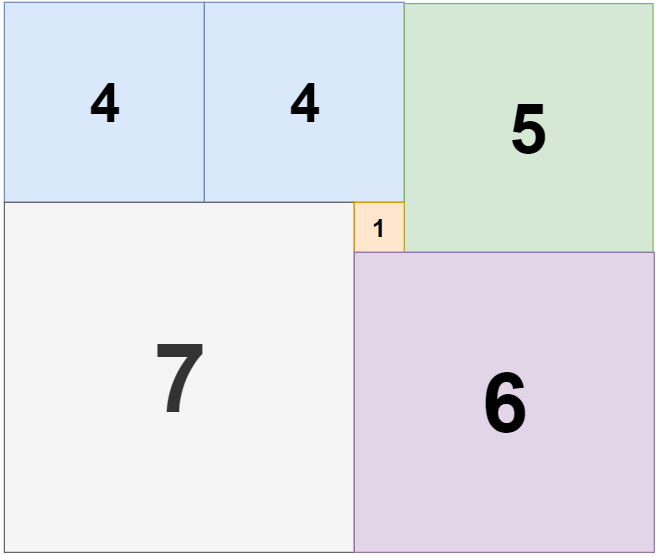
Input: n = 11, m = 13 Output: 6
Constraints:
1 <= n, m <= 13
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What are the maximum dimensions (length and width) of the rectangle?
- Are the dimensions of the rectangle always positive integers?
- If the rectangle cannot be tiled perfectly with squares, what should the function return? (e.g., null, -1, or throw an exception)
- Is there a preference for the side lengths of the squares used in the tiling (e.g., should I prioritize using larger squares first)?
- Should I return the number of squares required to tile the rectangle, or the dimensions of each square used in the tiling, or both?
Brute Force Solution
Approach
The core idea is to explore every possible way to tile the rectangle with squares. We recursively try different square sizes and placements, dividing the problem into smaller sub-rectangles. The best solution is the one using the fewest squares among all possible tilings.
Here's how the algorithm would work step-by-step:
- Start with the original rectangle.
- Try placing the largest possible square that fits inside the rectangle. The side of the square must be equal to the smaller side of the rectangle.
- This leaves you with one or two smaller rectangles (or none if the original rectangle was already a square).
- For each of the remaining rectangles, repeat the process of placing the largest possible square inside them.
- Continue this process until all rectangles are filled with squares. This represents one way to tile the original rectangle.
- Now, go back and try a slightly smaller square size than the largest possible square that could be placed initially. Repeat the whole process to create another tiling arrangement.
- Keep trying different initial square sizes and different arrangements for the remaining rectangles.
- Keep track of the number of squares used in each arrangement.
- Finally, compare all the tiling arrangements you created and choose the one that uses the fewest squares.
Code Implementation
def tiling_rectangle_brute_force(row_count, column_count):
# Memoization to avoid recomputing
memo = {}
def solve(current_row_count, current_column_count):
if (current_row_count, current_column_count) in memo:
return memo[(current_row_count, current_column_count)]
if current_row_count == current_column_count:
return 1
if current_row_count == 0 or current_column_count == 0:
return 0
minimum_squares = float('inf')
# Try placing the largest possible square
square_size = min(current_row_count, current_column_count)
#Explore tiling by placing max size square
squares_used = 1 + solve(current_row_count - square_size, current_column_count) if current_row_count > current_column_count else 1 + solve(current_row_count, current_column_count - square_size)
minimum_squares = min(minimum_squares, squares_used)
# Try different splitting options along rows
for split_row in range(1, current_row_count):
minimum_squares = min(minimum_squares, solve(split_row, current_column_count) + solve(current_row_count - split_row, current_column_count))
#Try different splitting option along cols
for split_column in range(1, current_column_count):
minimum_squares = min(minimum_squares, solve(current_row_count, split_column) + solve(current_row_count, current_column_count - split_column))
memo[(current_row_count, current_column_count)] = minimum_squares
return minimum_squares
return solve(row_count, column_count)Big(O) Analysis
Optimal Solution
Approach
The goal is to cover the rectangle with the fewest possible squares. The core idea is to break down the problem into smaller, manageable pieces by repeatedly cutting off the largest possible square until nothing is left. This reduces the problem size at each step.
Here's how the algorithm would work step-by-step:
- Imagine the rectangle you want to tile. Find the largest possible square that fits inside it.
- Cut that square out of the rectangle. Now you're left with either another rectangle or a square.
- If you're left with another rectangle, repeat the process: find the largest square that fits inside the remaining rectangle and cut it out.
- Keep doing this until you are left with nothing (that is, until the remaining shape is a square and you cut it out).
- Count how many squares you cut out in total. That's the smallest number of squares you can use to tile the original rectangle.
Code Implementation
def tiling_rectangle_with_squares(rectangle_length, rectangle_width):
number_of_squares = 0
# Use dynamic programming to store the minimum squares needed for sub-rectangles.
dp_table = {}
def min_squares(length, width):
if length == width:
return 1
if length > width:
length, width = width, length
if (length, width) in dp_table:
return dp_table[(length, width)]
minimum_squares_needed = float('inf')
# Iterate through all possible sizes of the first square.
for i in range(1, length + 1):
# Cutting the square horizontally.
horizontal_cut = min_squares(length - i, width) + 1
minimum_squares_needed = min(minimum_squares_needed, horizontal_cut)
# Cutting the square vertically.
vertical_cut = min_squares(length, width - i) + 1
minimum_squares_needed = min(minimum_squares_needed, vertical_cut)
# Store the result in the DP table for memoization.
dp_table[(length, width)] = minimum_squares_needed
return minimum_squares_needed
return min_squares(rectangle_length, rectangle_width)Big(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Zero width or height | Return 0 as no tiles are needed for a rectangle with zero dimension; handle it with a base case check. |
| Negative width or height | Return an error or throw an exception as rectangle dimensions cannot be negative; validate inputs at the beginning. |
| Width equals height (square) | Return 1, as only one square is needed to tile the area; handle this with a base case check. |
| Large width and height values leading to potential integer overflow during calculation. | Use long data types or consider alternative algorithms to prevent overflow when calculating tile counts. |
| Width or height being 1 | Return the other dimension, as it represents the number of 1x1 squares needed; handle this with a base case check. |
| Extremely different width and height (e.g., 1 and 1000) | Ensure the algorithm does not exceed time limit with large inputs and that recursion (if used) has appropriate base cases to prevent stack overflow. |
| Stack overflow with recursive calls for certain dimensions | Implement memoization to store previously calculated results and prevent redundant calculations in the recursive function to limit call depth. |
| Multiple optimal tiling solutions exist | The algorithm should return any one of the optimal solutions and not be concerned about which solution is returned as only minimum tiles are important. |