Trim a Binary Search Tree
MediumGiven the root of a binary search tree and the lowest and highest boundaries as low and high, trim the tree so that all its elements lies in [low, high]. Trimming the tree should not change the relative structure of the elements that will remain in the tree (i.e., any node's descendant should remain a descendant). It can be proven that there is a unique answer.
Return the root of the trimmed binary search tree. Note that the root may change depending on the given bounds.
Example 1:

Input: root = [1,0,2], low = 1, high = 2 Output: [1,null,2]
Example 2:
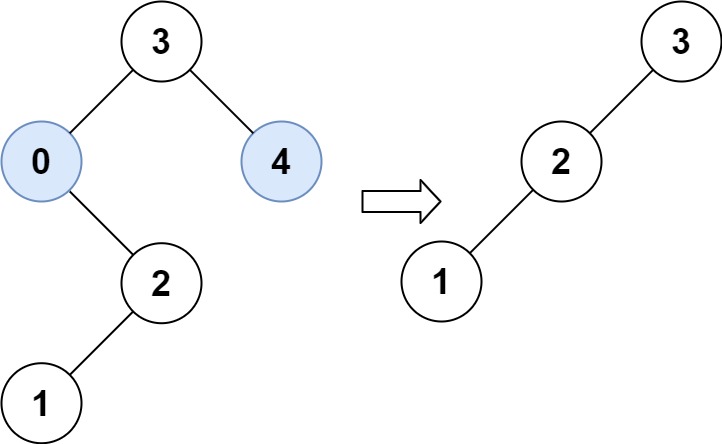
Input: root = [3,0,4,null,2,null,null,1], low = 1, high = 3 Output: [3,2,null,1]
Constraints:
- The number of nodes in the tree is in the range
[1, 104]. 0 <= Node.val <= 104- The value of each node in the tree is unique.
rootis guaranteed to be a valid binary search tree.0 <= low <= high <= 104
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What are the possible value ranges for the node values in the BST, as well as for low and high?
- Could the input tree be empty (root is null)? If so, what should I return?
- Are `low` and `high` guaranteed to be valid integers, and is `low` always less than or equal to `high`?
- If a node's value is equal to `low` or `high`, should it be included in the trimmed tree?
- Is the input guaranteed to be a valid Binary Search Tree?
Brute Force Solution
Approach
The most straightforward way to trim a binary search tree is to consider each node individually. We examine every node to determine if it falls within the specified range and remove those that don't, rebuilding the tree as needed.
Here's how the algorithm would work step-by-step:
- Start at the very top of the tree, the root node.
- Check if the current node's value is within the allowed range (between the low and high values).
- If the node's value is too small, completely remove that node and everything below it by replacing it with the right child.
- If the node's value is too big, completely remove that node and everything below it by replacing it with the left child.
- If the node's value is just right, then do the same check on the node to the left, and the node to the right. Essentially, keep going down the tree, repeating the process for each node.
- After checking all the nodes and removing the ones outside the range, you will have a trimmed tree that contains only the nodes with values within the specified range.
Code Implementation
def trim_a_binary_search_tree(root, low_value, high_value):
if not root:
return None
# If current node is out of range on the lower end
if root.val < low_value:
return trim_a_binary_search_tree(root.right, low_value, high_value)
# If current node is out of range on the higher end
if root.val > high_value:
return trim_a_binary_search_tree(root.left, low_value, high_value)
# Node value is within the range
# Need to trim the left and right subtrees
root.left = trim_a_binary_search_tree(root.left, low_value, high_value)
# Ensure only values within range are on right side
root.right = trim_a_binary_search_tree(root.right, low_value, high_value)
return rootBig(O) Analysis
Optimal Solution
Approach
The goal is to cut away parts of a search tree so only values within a certain range remain. We use the special properties of search trees to avoid looking at every single node, making the process much faster. By only exploring nodes that are potentially within the range, we dramatically cut down on unnecessary checks.
Here's how the algorithm would work step-by-step:
- Start at the very top of the tree.
- If the current node's value is too small, we know the entire left side of the tree is also too small, so we replace the current node with its right child (which is guaranteed to be within the allowed range or larger).
- If the current node's value is too big, we know the entire right side of the tree is also too big, so we replace the current node with its left child (which is guaranteed to be within the allowed range or smaller).
- If the current node's value is just right (within the desired range), we look at its left and right children and apply the same process to them.
- Keep repeating these steps going down the tree, adjusting the children of each node until everything outside the desired range is removed.
Code Implementation
def trim_bst(root_node, low_value, high_value):
if not root_node:
return None
if root_node.val < low_value:
# Node is too small, return right subtree
return trim_bst(root_node.right, low_value, high_value)
if root_node.val > high_value:
# Node is too large, return left subtree
return trim_bst(root_node.left, low_value, high_value)
# Node is within range, process subtrees
root_node.left = trim_bst(root_node.left, low_value, high_value)
# Trimming the right sub-tree
root_node.right = trim_bst(root_node.right, low_value, high_value)
return root_nodeBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| root is null | Return null immediately if the root is null, indicating an empty tree. |
| low equals high | Handle correctly by still performing the trim operation based on the single value in the range. |
| All nodes are smaller than low | The recursive calls should propagate null back up the tree, resulting in a null root. |
| All nodes are larger than high | The recursive calls should propagate null back up the tree, resulting in a null root. |
| low is smaller than the minimum value in the tree and high is greater than the maximum value in the tree | The function should return the original root because no nodes need to be trimmed. |
| A deeply unbalanced BST (e.g., a linked list structure) | Recursion might lead to stack overflow for extremely unbalanced trees, but the algorithm's correctness isn't affected. |
| Duplicate values within the valid range | The algorithm correctly handles duplicates because it operates based on range, not specific value uniqueness. |
| low or high is null | Ensure to gracefully handle null low or high values by considering them as negative or positive infinity respectively (depending on the language, proper null-aware handling would be required). |