Unique Binary Search Trees #16 Most Asked
MediumGiven an integer n, return the number of structurally unique BST's (binary search trees) which has exactly n nodes of unique values from 1 to n.
Example 1:
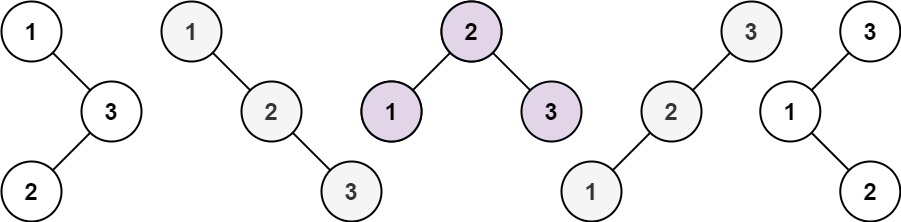
Input: n = 3 Output: 5
Example 2:
Input: n = 1 Output: 1
Constraints:
1 <= n <= 19
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What is the maximum possible value of 'n'? I want to understand the scale of the input and potential performance implications?
- Is 'n' guaranteed to be a non-negative integer?
- For n = 0, should I return 1 (representing an empty tree) or 0?
- Could you provide a small example (e.g., n = 3) and the expected output, to ensure my understanding of 'structurally unique' is correct?
- Are we only concerned with the *number* of structurally unique BSTs, or would I also need to provide the actual tree structures in a real-world scenario?
Brute Force Solution
Approach
The goal is to find the number of different Binary Search Trees (BSTs) you can build with a given number of nodes. The brute force method involves trying every single possible tree structure and counting the ones that follow the BST rules.
Here's how the algorithm would work step-by-step:
- For each number from 1 up to the given number of nodes, consider that number as the root of a potential BST.
- If a number is the root, the numbers smaller than it will form the left subtree, and the numbers bigger than it will form the right subtree.
- Now, for each possible left subtree, figure out all the different BST shapes it can have. Do the same for the right subtree.
- Each unique combination of a left subtree shape and a right subtree shape, along with the chosen root, gives us a unique BST.
- Add up the number of unique BSTs you can create for each possible root. This total is the final answer.
Code Implementation
def unique_binary_search_trees(number_of_nodes):
# Base case: no nodes or one node, only one possible BST
if number_of_nodes <= 1:
return 1
number_of_trees = 0
# Iterate through all possible root nodes
for root_node in range(1, number_of_nodes + 1):
#Calculate the number of nodes in the left and right subtrees.
left_subtree_nodes = root_node - 1
right_subtree_nodes = number_of_nodes - root_node
#Recursively calculate number of left and right subtrees.
number_of_left_subtrees = unique_binary_search_trees(left_subtree_nodes)
number_of_right_subtrees = unique_binary_search_trees(right_subtree_nodes)
#Multiply subtrees for combinations
number_of_trees += number_of_left_subtrees * number_of_right_subtrees
return number_of_treesBig(O) Analysis
Optimal Solution
Approach
The key is to realize the number of unique binary search trees for a given number is related to the numbers for smaller values. We can build up the answer from the bottom, using previous calculations to avoid recalculating the same things multiple times.
Here's how the algorithm would work step-by-step:
- Start by figuring out the answer for a very small number, like zero or one. These are your base cases and will be simple to calculate.
- Now, consider a larger number. Imagine each number from one up to that larger number being the 'root' of a binary search tree.
- For each possible root, figure out how many numbers are smaller (on the left) and how many are bigger (on the right).
- Use the answers you already calculated for those smaller 'left' and 'right' numbers. Multiply them together to find how many tree structures are possible for *that* specific root.
- Add up the number of trees possible for *each* root. That's the total number of unique binary search trees for your larger number.
- Repeat this process for all the numbers up to the target number, storing each result as you go. This way, you never have to recalculate the same thing twice. You're building the answer bit by bit, using what you've already figured out.
Code Implementation
def unique_binary_search_trees(number):
number_of_trees = [0] * (number + 1)
number_of_trees[0] = 1
number_of_trees[1] = 1
for nodes_count in range(2, number + 1):
# Iterate through all possible roots for the BST
for root_node in range(1, nodes_count + 1):
# Calculate the number of nodes in the left and right subtrees
left_subtree_nodes = root_node - 1
right_subtree_nodes = nodes_count - root_node
# Sum up the number of trees with each node as the root.
number_of_trees[nodes_count] += (number_of_trees[left_subtree_nodes] *
number_of_trees[right_subtree_nodes])
# Result is stored at the index of our target number
return number_of_trees[number]Big(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| n = 0 | Return 1, as an empty tree is considered a valid BST. |
| n = 1 | Return 1, as a single node tree is a valid BST. |
| n = 2 | Return 2, representing the two possible BST structures. |
| n is a large number that could lead to integer overflow | Use a data type with sufficient range (e.g., long in Java/C++) or implement overflow checking. |
| Check for stack overflow with recursive solutions for large n | Consider using dynamic programming (bottom-up approach) to avoid deep recursion and stack overflow. |
| Negative input for n | Throw an IllegalArgumentException or return 0, as the input represents the number of nodes, which cannot be negative. |
| n approaching the maximum integer value | Verify that intermediate calculations within the algorithm do not exceed the maximum integer value. |
| Input with extremely skewed BST structures | The Catalan number-based solution addresses all possible structural variations, including heavily skewed trees. |