Walking Robot Simulation II

Medium

Block

0 views

Topics:

Arrays

A width x height grid is on an XY-plane with the bottom-left cell at (0, 0) and the top-right cell at (width - 1, height - 1). The grid is aligned with the four cardinal directions ("North", "East", "South", and "West"). A robot is initially at cell (0, 0) facing direction "East".

The robot can be instructed to move for a specific number of steps. For each step, it does the following.

Attempts to move forward one cell in the direction it is facing.
If the cell the robot is moving to is out of bounds, the robot instead turns 90 degrees counterclockwise and retries the step.

After the robot finishes moving the number of steps required, it stops and awaits the next instruction.

Implement the Robot class:

Robot(int width, int height) Initializes the width x height grid with the robot at (0, 0) facing "East".
void step(int num) Instructs the robot to move forward num steps.
int[] getPos() Returns the current cell the robot is at, as an array of length 2, [x, y].
String getDir() Returns the current direction of the robot, "North", "East", "South", or "West".

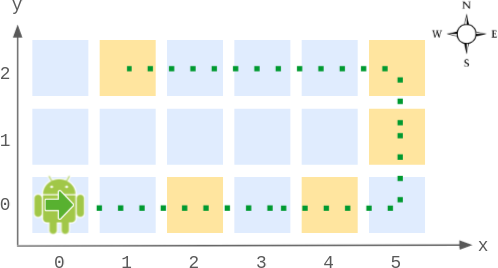
Example 1:

Input
["Robot", "step", "step", "getPos", "getDir", "step", "step", "step", "getPos", "getDir"]
[[6, 3], [2], [2], [], [], [2], [1], [4], [], []]
Output
[null, null, null, [4, 0], "East", null, null, null, [1, 2], "West"]

Explanation
Robot robot = new Robot(6, 3); // Initialize the grid and the robot at (0, 0) facing East.
robot.step(2);  // It moves two steps East to (2, 0), and faces East.
robot.step(2);  // It moves two steps East to (4, 0), and faces East.
robot.getPos(); // return [4, 0]
robot.getDir(); // return "East"
robot.step(2);  // It moves one step East to (5, 0), and faces East.
                // Moving the next step East would be out of bounds, so it turns and faces North.
                // Then, it moves one step North to (5, 1), and faces North.
robot.step(1);  // It moves one step North to (5, 2), and faces North (not West).
robot.step(4);  // Moving the next step North would be out of bounds, so it turns and faces West.
                // Then, it moves four steps West to (1, 2), and faces West.
robot.getPos(); // return [1, 2]
robot.getDir(); // return "West"

Constraints:

2 <= width, height <= 100
1 <= num <= 10⁵
At most 10⁴ calls in total will be made to step, getPos, and getDir.

Try coding it in LeetCode

Walking Robot Simulation II

Medium

Block

0 views

Topics:

Arrays

A width x height grid is on an XY-plane with the bottom-left cell at (0, 0) and the top-right cell at (width - 1, height - 1). The grid is aligned with the four cardinal directions ("North", "East", "South", and "West"). A robot is initially at cell (0, 0) facing direction "East".

The robot can be instructed to move for a specific number of steps. For each step, it does the following.

Attempts to move forward one cell in the direction it is facing.
If the cell the robot is moving to is out of bounds, the robot instead turns 90 degrees counterclockwise and retries the step.

After the robot finishes moving the number of steps required, it stops and awaits the next instruction.

Implement the Robot class:

Robot(int width, int height) Initializes the width x height grid with the robot at (0, 0) facing "East".
void step(int num) Instructs the robot to move forward num steps.
int[] getPos() Returns the current cell the robot is at, as an array of length 2, [x, y].
String getDir() Returns the current direction of the robot, "North", "East", "South", or "West".

Example 1:

Input
["Robot", "step", "step", "getPos", "getDir", "step", "step", "step", "getPos", "getDir"]
[[6, 3], [2], [2], [], [], [2], [1], [4], [], []]
Output
[null, null, null, [4, 0], "East", null, null, null, [1, 2], "West"]

Explanation
Robot robot = new Robot(6, 3); // Initialize the grid and the robot at (0, 0) facing East.
robot.step(2);  // It moves two steps East to (2, 0), and faces East.
robot.step(2);  // It moves two steps East to (4, 0), and faces East.
robot.getPos(); // return [4, 0]
robot.getDir(); // return "East"
robot.step(2);  // It moves one step East to (5, 0), and faces East.
                // Moving the next step East would be out of bounds, so it turns and faces North.
                // Then, it moves one step North to (5, 1), and faces North.
robot.step(1);  // It moves one step North to (5, 2), and faces North (not West).
robot.step(4);  // Moving the next step North would be out of bounds, so it turns and faces West.
                // Then, it moves four steps West to (1, 2), and faces West.
robot.getPos(); // return [1, 2]
robot.getDir(); // return "West"

Constraints:

2 <= width, height <= 100
1 <= num <= 10⁵
At most 10⁴ calls in total will be made to step, getPos, and getDir.

Try coding it in LeetCode

Solution

Clarifying Questions

When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:

What are the constraints on the dimensions of the grid (width and height)? Are they positive integers?
Can the starting position (0, 0) be outside the grid? If so, what should happen?
Is it possible for the width or height to be zero, resulting in an empty grid? If so, what should the initial direction and position be?
If the robot encounters the same cell and direction multiple times, how should the simulation behave? Should it loop infinitely, or is there an expected output?
Is there a maximum number of steps that the robot will be asked to move? This could help me determine if I need to worry about potential integer overflow issues in tracking the position.

Brute Force Solution

Approach

Imagine a robot walking around a rectangular grid. The brute force approach simulates the robot's movement step by step for every possible command it receives. It meticulously tracks the robot's position after each move to figure out where it ends up.

Here's how the algorithm would work step-by-step:

Start the robot at its initial position on the grid.
For each command the robot receives, move the robot one step at a time in the direction it's currently facing.
If the robot tries to move off the grid, make it turn appropriately and then try moving one step again.
Keep repeating the single-step movement until the robot has moved the number of steps indicated by the current command.
Record the robot's final position after executing all the commands.
That final position is the result of our brute force simulation.

Code Implementation

class WalkingRobotSimulationII:
    def __init__(self, width: int, height: int):
        self.width = width
        self.height = height
        self.current_position_x = 0
        self.current_position_y = 0
        self.direction_index = 0 # 0: East, 1: North, 2: West, 3: South
        self.directions = [(1, 0), (0, 1), (-1, 0), (0, -1)]

    def step(self, number_of_steps: int) -> None:
        for _ in range(number_of_steps):
            next_position_x = self.current_position_x + self.directions[self.direction_index][0]
            next_position_y = self.current_position_y + self.directions[self.direction_index][1]

            # Determine if next step is valid and move or rotate if invalid
            if 0 <= next_position_x < self.width and 0 <= next_position_y < self.height:
                self.current_position_x = next_position_x
                self.current_position_y = next_position_y
            else:
                self.direction_index = (self.direction_index + 1) % 4

                next_position_x = self.current_position_x + self.directions[self.direction_index][0]
                next_position_y = self.current_position_y + self.directions[self.direction_index][1]

                if 0 <= next_position_x < self.width and 0 <= next_position_y < self.height:
                    self.current_position_x = next_position_x
                    self.current_position_y = next_position_y

                #Handle edge case where robot may be in a corner
                else:
                    break

    def getPos(self) -> list[int]:
        return [self.current_position_x, self.current_position_y]

    def getDir(self) -> str:
        # Map direction index to string representation
        if self.direction_index == 0:
            return "East"
        elif self.direction_index == 1:
            return "North"
        elif self.direction_index == 2:
            return "West"

        # If all the above checks failed then return South as direction
        else:
            return "South"

Big(O) Analysis

Time Complexity

O(m*c) – Let m be the total number of commands and c be the maximum number of steps in any single command. For each command, the robot moves one step at a time. In the worst case, each command requires the robot to take its full number of steps 'c' because it could potentially take a number of steps equal to the command's value. Therefore, the algorithm iterates through each of the m commands, and for each command, it may execute up to 'c' steps, resulting in m * c operations. Thus, the time complexity is O(m*c).

Space Complexity

O(1) – The brute force approach described simulates the robot's movement step-by-step without storing any intermediate states or visited locations. It only uses a fixed number of variables to store the current position of the robot and the current direction. Therefore, the auxiliary space required is constant and independent of the number of commands or the grid size, which we can consider as N.

Optimal Solution

Approach

The robot moves along the perimeter of a rectangular grid. We can simulate this movement efficiently by thinking of the perimeter as a cycle and tracking the robot's position along it, rather than directly updating its coordinates after each move. This avoids repeating calculations and improves performance.

Here's how the algorithm would work step-by-step:

First, calculate the total length of the path the robot will walk, which is the perimeter of the rectangle.
Store the dimensions of the rectangle, as these define the boundaries of the path.
Keep track of the robot's current location along the perimeter, not just its (x, y) coordinates.
When the robot needs to move a certain number of steps, calculate where it will end up along the perimeter after taking those steps. If the number of steps is larger than the perimeter, find the remainder after dividing by the perimeter, as the robot will effectively loop around.
Determine the robot's final (x, y) coordinates based on its new location along the perimeter. You can do this by checking which side of the rectangle the robot is on and calculating the position along that side. Consider the order of traversal (east, north, west, south) as this influences coordinate calculations.
Update the stored location along the perimeter with the new location for the next move. This ensures that the next move calculation starts from the correct position.

Code Implementation

class WalkingRobot:
    def __init__(self, width: int, height: int):
        self.width_limit = width
        self.height_limit = height
        self.current_x = 0
        self.current_y = 0
        self.direction_index = 0
        self.directions = ["East", "North", "West", "South"]

        # Calculate the perimeter of the rectangle
        self.perimeter = 2 * (width + height) - 4
        self.current_position = 0

    def step(self, number_of_steps: int) -> None:
        # Normalize steps to account for looping around the perimeter.
        number_of_steps %= self.perimeter

        self.current_position = (self.current_position + number_of_steps) % self.perimeter

        current_width = self.width_limit - 1
        current_height = self.height_limit - 1

        if self.current_position <= current_width:
            self.current_x = self.current_position
            self.current_y = 0
            self.direction_index = 0

        elif self.current_position <= current_width + current_height:
            # Determine position on the north side.
            self.current_x = current_width
            self.current_y = self.current_position - current_width
            self.direction_index = 1

        elif self.current_position <= current_width * 2 + current_height:
            self.current_x = current_width - (self.current_position - (current_width + current_height))
            self.current_y = current_height
            self.direction_index = 2

        else:
            # Calculate the remaining distance to find the y-coordinate.
            self.current_x = 0
            self.current_y = current_height - (self.current_position - (2 * current_width + current_height))
            self.direction_index = 3

    def getPos(self) -> list[int]:
        return [self.current_x, self.current_y]

    def getDir(self) -> str:
        return self.directions[self.direction_index]

Big(O) Analysis

Time Complexity

O(1) – The provided solution involves calculating the perimeter, storing dimensions, and updating the robot's position. Regardless of the number of steps the robot takes, the calculations performed (perimeter calculation, modulo operation, and coordinate determination) involve a fixed number of arithmetic and comparison operations. Therefore, the time complexity does not depend on the input size (number of steps) and remains constant, resulting in O(1).

Space Complexity

O(1) – The solution stores a few variables: the dimensions of the rectangle (width and height), the current location along the perimeter, and possibly a few temporary variables for calculations. These variables consume a fixed amount of memory regardless of how long the robot moves or the perimeter's length. Therefore, the auxiliary space required is constant and does not scale with the input size N.

Edge Cases

Case	How to Handle
Zero width or height in constructor	The constructor should probably throw an exception or error if either dimension is zero as the robot cannot move.
Single step causes robot to complete a full loop	Modulo operations and current direction tracking should correctly handle complete loops without issues.
Large width and height values leading to integer overflow during distance calculations	Ensure that the data type used for distance calculations (perimeter) is large enough to prevent overflow (e.g., long in Java/C++).
Multiple consecutive calls to move() results in several full loops	The code should appropriately use the modulo operator to manage large step counts and wrap around the perimeter accurately.
Initial direction is not NORTH, EAST, SOUTH, or WEST	The direction should be properly initialized and checked in the constructor, setting to a default if an invalid direction is provided.
Empty path (width=1, height=1)	If width=1 and height=1, define an appropriate boundary and edge case to avoid infinite recursion.
Move() called after the robot has been fully around the perimeter.	The remainder operator in move should handle this correctly allowing the robot to retrace the same path.
Very large number of move calls with relatively small width/height	The modulo operator used when computing the remaining steps should avoid performance degradation with an extremely large number of moves.