Water Bottles II
MediumYou are given two integers numBottles and numExchange.
numBottles represents the number of full water bottles that you initially have. In one operation, you can perform one of the following operations:
- Drink any number of full water bottles turning them into empty bottles.
- Exchange
numExchangeempty bottles with one full water bottle. Then, increasenumExchangeby one.
Note that you cannot exchange multiple batches of empty bottles for the same value of numExchange. For example, if numBottles == 3 and numExchange == 1, you cannot exchange 3 empty water bottles for 3 full bottles.
Return the maximum number of water bottles you can drink.
Example 1:

Input: numBottles = 13, numExchange = 6 Output: 15 Explanation: The table above shows the number of full water bottles, empty water bottles, the value of numExchange, and the number of bottles drunk.
Example 2:
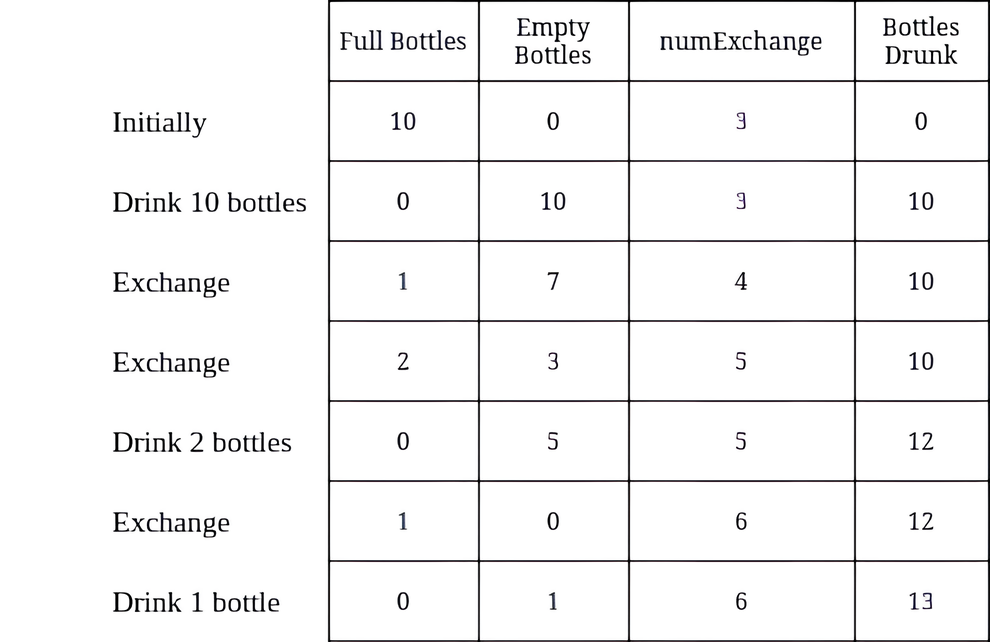
Input: numBottles = 10, numExchange = 3 Output: 13 Explanation: The table above shows the number of full water bottles, empty water bottles, the value of numExchange, and the number of bottles drunk.
Constraints:
1 <= numBottles <= 1001 <= numExchange <= 100
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What are the possible ranges for `totalBottles`, `bottlesToExchange`, and `exchangeProfit`? Can any of them be zero or negative?
- If `bottlesToExchange` is greater than `totalBottles` initially, meaning I cannot exchange any bottles at all, what should the return value be?
- Is `exchangeProfit` the profit *per* exchange, or a fixed profit earned for *all* exchanges?
- If `bottlesToExchange` is 1, will the exchange continue indefinitely, or is there an intended stopping condition?
- Is integer overflow a concern given the potential ranges of the input variables?
Brute Force Solution
Approach
The problem asks us to find the maximum number of water bottles we can fill given different bottle sizes and a limited amount of water. The brute force strategy tries every possible combination of filling bottles, checking if we have enough water.
Here's how the algorithm would work step-by-step:
- Start by trying to fill only the first bottle type, as many as possible.
- Then, try all possibilities of filling just the second bottle type as many as possible instead, ignoring the first type completely.
- Next, explore all combinations where we fill some of the first bottle type and some of the second bottle type, up to their maximum possible quantities.
- Continue this process, considering every possible quantity of each bottle type, one at a time. Then two at a time. Then three at a time, and so on until we include all possible bottle type quantities.
- For each combination of filled bottles, calculate the total amount of water used.
- If the total water used is within the limit, count the number of bottles filled in that combination and remember it.
- If the total water used exceeds the limit, discard that combination and move on.
- After checking all possible combinations, find the combination that resulted in the largest number of bottles filled, while still staying within the water limit. That's our answer.
Code Implementation
def water_bottles_brute_force(number_of_bottle_types, bottle_volumes, bottle_counts, total_volume):
maximum_bottles = 0
# Iterate through all possible combinations of bottle counts
def find_best_combination(current_bottle_index, current_volume, current_bottles):
nonlocal maximum_bottles
# If we've considered all bottle types
if current_bottle_index == number_of_bottle_types:
if current_volume <= total_volume:
maximum_bottles = max(maximum_bottles, current_bottles)
return
# Iterate through all possible quantities of the current bottle type
for bottle_quantity in range(bottle_counts[current_bottle_index] + 1):
new_volume = current_volume + bottle_quantity * bottle_volumes[current_bottle_index]
# Optimization: Skip if the volume exceeds the limit
if new_volume > total_volume:
continue
find_best_combination(
current_bottle_index + 1,
new_volume,
current_bottles + bottle_quantity
)
# Start the recursive search from the first bottle type
find_best_combination(0, 0, 0)
return maximum_bottlesBig(O) Analysis
Optimal Solution
Approach
This problem involves figuring out the maximum number of water bottles you can drink given some constraints. The optimal approach avoids recalculating the same information repeatedly by storing results in a smart way.
Here's how the algorithm would work step-by-step:
- Think of the problem as a series of choices: how many times to refill bottle A, how many times to refill bottle B, and so on.
- Recognize that if you've already figured out the best answer for a certain amount of water in bottle A and bottle B, you don't need to recalculate it later.
- Create a system (like a chart) to remember the best answer for every possible combination of water levels in the bottles.
- Start by finding the best answer for the smallest possible amounts of water.
- Then, use those answers to figure out the best answer for slightly larger amounts, building up your chart along the way.
- Whenever you need to know the best answer for a combination you've already solved, just look it up in your chart instead of recalculating it.
- Continue filling out your chart until you've figured out the best answer for the maximum allowed amounts of water. That will be your final answer.
- This way, you only calculate each answer once, making the process much faster.
Code Implementation
def max_water_bottles(number_of_bottles, empty_bottles_to_exchange, new_bottles):
best_result_so_far = 0
current_bottles = number_of_bottles
current_drunk_bottles = 0
while current_bottles > 0:
# Drink all current bottles.
current_drunk_bottles += current_bottles
# Calculate empty bottles.
empty_bottles = current_bottles
# Exchange empty bottles for new bottles.
new_bottles_from_exchange = empty_bottles // empty_bottles_to_exchange
#Remaining bottles after potential exchange
remaining_empty_bottles = empty_bottles % empty_bottles_to_exchange
#Update current total of bottles available
current_bottles = new_bottles_from_exchange * new_bottles + remaining_empty_bottles
# Update the best result if needed
best_result_so_far = current_drunk_bottles
return best_result_so_farBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| totalBottles is zero | Return 0 because you cannot drink any water bottles if you start with none. |
| bottlesToExchange is zero | Return totalBottles, as you can never exchange for more bottles, so you only drink the initial amount. |
| bottlesToExchange is one | The loop becomes infinite unless specifically handled, so return Integer.MAX_VALUE or handle specifically to avoid overflow/infinite loops. |
| totalBottles is negative | Throw an IllegalArgumentException or return 0 as you can't have negative bottles. |
| bottlesToExchange is negative | Throw an IllegalArgumentException, as it's illogical to exchange for a negative number of bottles. |
| exchangeProfit is zero | This does not change the logic; the code will still function and produce a correct result based on drinking and exchanging bottles without profit. |
| Large totalBottles and small bottlesToExchange may cause integer overflow when calculating exchanged bottles. | Use long to store intermediate results when calculating the number of exchanged bottles to avoid overflow. |
| totalBottles is equal to bottlesToExchange | Drink all initial bottles, then exchange for one more bottle, and then drink that one too, returning totalBottles + 1. |