Convert Binary Number in a Linked List to Integer
EasyGiven head which is a reference node to a singly-linked list. The value of each node in the linked list is either 0 or 1. The linked list holds the binary representation of a number.
Return the decimal value of the number in the linked list.
The most significant bit is at the head of the linked list.
Example 1:
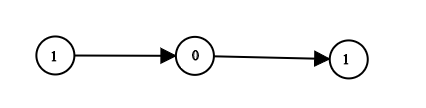
Input: head = [1,0,1] Output: 5 Explanation: (101) in base 2 = (5) in base 10
Example 2:
Input: head = [0] Output: 0
Constraints:
- The Linked List is not empty.
- Number of nodes will not exceed
30. - Each node's value is either
0or1.
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- Can the linked list be empty or contain null nodes?
- What is the maximum length of the linked list? Is there a limit to the magnitude of the resulting integer?
- Are the node values guaranteed to be either 0 or 1, or could there be other values?
- How should I handle potential overflow if the binary number is very large?
- Is memory allocation a constraint, or can I use additional data structures if needed?
Brute Force Solution
Approach
We're given a linked list that represents a binary number, and we need to find its decimal equivalent. The brute force way converts the binary number, bit by bit, into a decimal number by essentially simulating the manual conversion process.
Here's how the algorithm would work step-by-step:
- Start at the beginning of the linked list, which represents the most significant bit of the binary number.
- Initialize a decimal number to zero.
- For each bit in the linked list, starting from the beginning, double the current decimal number.
- Then, add the value of the current bit (0 or 1) to the decimal number.
- Move to the next bit in the linked list and repeat the previous two steps until you reach the end of the list.
- The final decimal number is the answer.
Code Implementation
def convert_binary_linked_list_to_integer(head):
decimal_value = 0
current_node = head
while current_node:
# Double the current decimal value to shift bits left
decimal_value *= 2
# Add the current bit's value to the decimal number
decimal_value += current_node.val
# Move to the next node in the linked list
current_node = current_node.next
return decimal_valueBig(O) Analysis
Optimal Solution
Approach
The problem asks us to treat a linked list like a binary number and find its decimal value. The most efficient method processes the binary number bit by bit, using the properties of binary representation to quickly calculate the result. We avoid storing the entire number or doing unnecessary calculations.
Here's how the algorithm would work step-by-step:
- Start with a result of zero.
- Look at each number in the linked list, one at a time, from beginning to end.
- For each number, double the current result.
- If the current number is one, add one to the result.
- Move to the next number in the list and repeat steps 3 and 4 until you reach the end of the list.
- The final result is the decimal representation of the binary number in the linked list.
Code Implementation
class ListNode:
def __init__(self, val=0, next=None):
self.val = val
self.next = next
def get_decimal_value(head):
decimal_value = 0
current_node = head
while current_node:
# Double the current value, shifting bits to the left
decimal_value = decimal_value * 2
# Add 1 if the current node's value is 1
if current_node.val == 1:
decimal_value = decimal_value + 1
current_node = current_node.next
return decimal_valueBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Empty linked list (head is null) | Return 0 immediately as an empty list represents the decimal value 0. |
| Linked list with a single node containing 0 | The algorithm should correctly return 0. |
| Linked list with a single node containing 1 | The algorithm should correctly return 1. |
| Very long linked list potentially leading to integer overflow | Use a data type with a larger range than a standard integer (e.g., long) or calculate modulo a large prime to avoid overflow if the problem specifies a modulo operation should be used. |
| Linked list with all 0s | The algorithm should correctly return 0. |
| Linked list with all 1s | The algorithm should correctly calculate the decimal representation (2^n - 1). |
| Linked list starting with multiple consecutive 0s | These leading zeros should not affect the final decimal value after the first 1. |
| Null nodes present within the linked list (invalid input) | Throw an exception or return an error code to indicate invalid input since linked lists should not have null nodes between the head and tail. |