Largest Rectangle in Histogram
HardGiven an array of integers heights representing the histogram's bar height where the width of each bar is 1, return the area of the largest rectangle in the histogram.
Example 1:
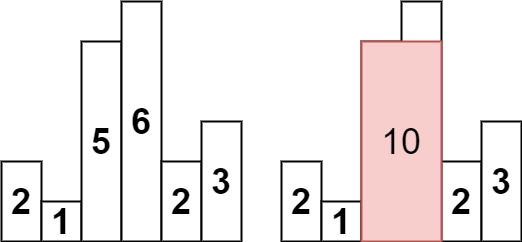
Input: heights = [2,1,5,6,2,3] Output: 10 Explanation: The above is a histogram where width of each bar is 1. The largest rectangle is shown in the red area, which has an area = 10 units.
Example 2:
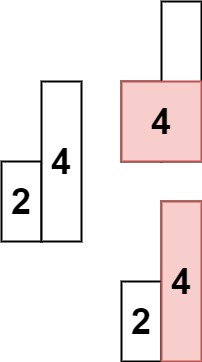
Input: heights = [2,4] Output: 4
Constraints:
1 <= heights.length <= 1050 <= heights[i] <= 104
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What is the expected range of values for the heights in the input array? Could they be negative or zero?
- What should I return if the input array is empty or null?
- Are there any limits on the size (number of bars) of the histogram? I'm thinking about potential space and time complexity implications.
- In the case of multiple rectangles with the same largest area, is any of them acceptable to return?
- Are the heights always integers, or could they be floating-point numbers?
Brute Force Solution
Approach
The brute force strategy finds the biggest rectangle by checking every possible rectangle you could make. It’s like trying every combination of building blocks to see which one creates the biggest structure. We go through each possibility, calculate its area, and remember the largest area we've seen so far.
Here's how the algorithm would work step-by-step:
- For every bar in the histogram, consider it as the shortest bar in a potential rectangle.
- For each of these 'shortest bar' candidates, look at all the bars to its left and right to see how wide we can make a rectangle.
- The width of the rectangle is determined by how many bars are at least as tall as our 'shortest bar'.
- Calculate the area of this rectangle (height times width).
- Compare this area with the biggest area we've found so far and update the 'biggest area' if needed.
- After checking all possible 'shortest bars' and their corresponding rectangles, the 'biggest area' we've kept track of is the answer.
Code Implementation
def largest_rectangle_brute_force(heights):
max_area = 0
number_of_heights = len(heights)
for current_index in range(number_of_heights):
# Consider each bar as the shortest bar.
shortest_bar = heights[current_index]
current_area = shortest_bar
max_area = max(max_area, current_area)
left_index = current_index - 1
right_index = current_index + 1
width = 1
# Expand to the left while heights are >= shortest bar.
while left_index >= 0 and heights[left_index] >= shortest_bar:
width += 1
current_area = shortest_bar * width
max_area = max(max_area, current_area)
left_index -= 1
# Expand to the right while heights are >= shortest bar.
width = current_index - left_index - 1
while right_index < number_of_heights and heights[right_index] >= shortest_bar:
width += 1
current_area = shortest_bar * width
#Track maximum area
max_area = max(max_area, current_area)
right_index += 1
#Consider the current height as min and determine width.
current_width = right_index - left_index - 1
current_area = shortest_bar * current_width
#Update the max area if necessary.
max_area = max(max_area, current_area)
for compare_index in range(current_index + 1, number_of_heights):
# Find the minimum height in the selected range
shortest_bar = min(shortest_bar, heights[compare_index])
# Calculate area for the current sub-rectangle
current_width = compare_index - current_index + 1
current_area = shortest_bar * current_width
max_area = max(max_area, current_area)
return max_areaBig(O) Analysis
Optimal Solution
Approach
To find the largest rectangle, the clever way is to efficiently keep track of potential rectangles as we go. We avoid unnecessary calculations by focusing on when a rectangle's height is limited by a smaller bar.
Here's how the algorithm would work step-by-step:
- Imagine you're walking across the bars from left to right, and you're tracking the possibility of forming rectangles.
- Keep adding bars to your potential rectangle as long as the bars are getting taller or staying the same height. These bars could be part of our best rectangle.
- If you find a bar that's shorter than the bar you were just looking at, this means the potential rectangle ending at that previous bar is now limited. That means you can now calculate the area of that rectangle using that bar's height.
- When you calculate the area of a rectangle, remember what column that height started from so you can find its width.
- Keep doing this, and when you encounter smaller bars, calculate the area of rectangles as needed, always figuring out which rectangle is the biggest you've found so far.
- At the end, remember to do a final check to calculate areas for any rectangles that are still in consideration.
Code Implementation
def largestRectangleArea(heights):
max_area = 0
stack = [] # Store (index, height) pairs
for i, height in enumerate(heights):
start_index = i
while stack and stack[-1][1] > height:
index, current_height = stack.pop()
max_area = max(max_area, current_height * (i - index))
start_index = index # Extend potential start
stack.append((start_index, height))
# Keep track of possible rectangles
# Calculate remaining areas in the stack
for index, height in stack:
max_area = max(max_area, height * (len(heights) - index))
return max_area
Big(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Empty input array | Return 0 immediately as no rectangle can exist. |
| Input array with one element | Return the value of the single element as it represents the largest possible rectangle. |
| Input array with all elements being 0 | Return 0 as the area of the largest rectangle will be zero. |
| Input array with all elements being the same positive value | Return the value multiplied by the number of elements (height * width). |
| Input array sorted in ascending order | Algorithm should correctly calculate area considering all heights from left to right when iterating or pushing/popping from stack. |
| Input array sorted in descending order | Algorithm should correctly calculate area when popping heights from stack and calculating the rectangle areas. |
| Large input array to test for time complexity (e.g., 10^5 elements) | The solution must be O(n) using a stack to ensure it completes within a reasonable time. |
| Input array contains large height values that could lead to integer overflow | Use a data type like 'long' to store intermediate area calculations to prevent potential integer overflow. |