Number of Flowers in Full Bloom

Hard

Roblox

0 views

Topics:

ArraysBinary Search

You are given a 0-indexed 2D integer array flowers, where flowers[i] = [start_i, end_i] means the i^th flower will be in full bloom from start_i to end_i (inclusive). You are also given a 0-indexed integer array people of size n, where people[i] is the time that the i^th person will arrive to see the flowers.

Return an integer array answer of size n, where answer[i] is the number of flowers that are in full bloom when the i^th person arrives.

Example 1:

Input: flowers = [[1,6],[3,7],[9,12],[4,13]], people = [2,3,7,11]
Output: [1,2,2,2]
Explanation: The figure above shows the times when the flowers are in full bloom and when the people arrive.
For each person, we return the number of flowers in full bloom during their arrival.

Example 2:

Input: flowers = [[1,10],[3,3]], people = [3,3,2]
Output: [2,2,1]
Explanation: The figure above shows the times when the flowers are in full bloom and when the people arrive.
For each person, we return the number of flowers in full bloom during their arrival.

Constraints:

1 <= flowers.length <= 5 * 10⁴
flowers[i].length == 2
1 <= start_i <= end_i <= 10⁹
1 <= people.length <= 5 * 10⁴
1 <= people[i] <= 10⁹

Number of Flowers in Full Bloom

Hard

Roblox

0 views

Topics:

ArraysBinary Search

You are given a 0-indexed 2D integer array flowers, where flowers[i] = [start_i, end_i] means the i^th flower will be in full bloom from start_i to end_i (inclusive). You are also given a 0-indexed integer array people of size n, where people[i] is the time that the i^th person will arrive to see the flowers.

Return an integer array answer of size n, where answer[i] is the number of flowers that are in full bloom when the i^th person arrives.

Example 1:

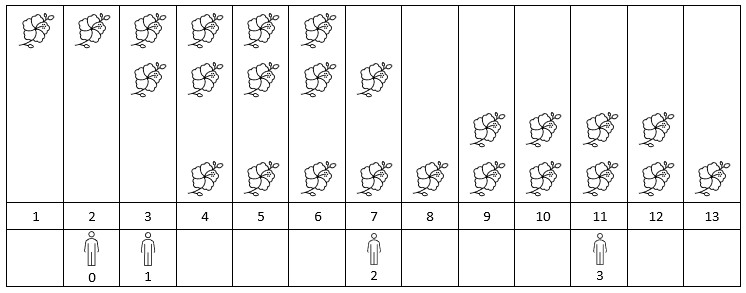
Input: flowers = [[1,6],[3,7],[9,12],[4,13]], people = [2,3,7,11]
Output: [1,2,2,2]
Explanation: The figure above shows the times when the flowers are in full bloom and when the people arrive.
For each person, we return the number of flowers in full bloom during their arrival.

Example 2:

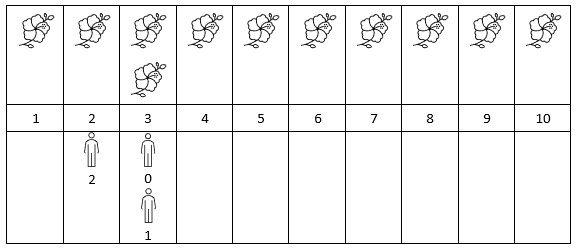
Input: flowers = [[1,10],[3,3]], people = [3,3,2]
Output: [2,2,1]
Explanation: The figure above shows the times when the flowers are in full bloom and when the people arrive.
For each person, we return the number of flowers in full bloom during their arrival.

Constraints:

1 <= flowers.length <= 5 * 10⁴
flowers[i].length == 2
1 <= start_i <= end_i <= 10⁹
1 <= people.length <= 5 * 10⁴
1 <= people[i] <= 10⁹

Solution

Clarifying Questions

When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:

What are the maximum sizes of the `flowers` and `people` arrays, and what is the maximum value for `start_i`, `end_i`, and elements in `people`?
Can the `start_i` and `end_i` values in a `flowers` entry be equal, and if so, what does that represent?
Is it possible for `start_i` to be greater than `end_i` in a `flowers` entry, and if so, how should I handle it?
What should the returned array contain if the `flowers` array is empty, or if no flowers are in bloom at a given person's arrival time?
Are the `start_i` and `end_i` values inclusive? For example, if a person arrives exactly at `start_i` or `end_i`, is the flower considered in bloom?

Brute Force Solution

Approach

The brute force approach to finding the number of blooming flowers for each person's arrival time involves checking each person individually. For each person, we will examine all the flower blooming periods to see if the person arrived during the bloom.

Here's how the algorithm would work step-by-step:

Take the first person's arrival time.
Go through each blooming period, one by one.
For each blooming period, check if the person's arrival time falls within that period (meaning the person arrived while that flower was blooming).
If the person arrived during the bloom, increase a counter for that person by one.
Repeat the process of checking all blooming periods for that first person until we have examined every single bloom.
Now that we've checked all flowers for the first person, we know how many flowers were blooming when they arrived. Write this number down.
Repeat steps 1-6 for every other person in the group.
After repeating steps for all the people, you will have the count of blooming flowers for each person.

Code Implementation

def number_of_flowers_in_full_bloom_brute_force(flowers, people):
    results = []
    for person_arrival_time in people:
        number_of_flowers_blooming = 0
        # Iterate through each flower's bloom period.
        for flower in flowers:

            bloom_start = flower[0]
            bloom_end = flower[1]
            # Check if the person arrived during the flower's bloom.
            if bloom_start <= person_arrival_time <= bloom_end:
                number_of_flowers_blooming += 1

        results.append(number_of_flowers_blooming)

    return results

Big(O) Analysis

Time Complexity

O(m*n) – The algorithm iterates through each person in the persons array, which has a size of n. For each person, it iterates through the entire flowers array, which has a size of m, to determine how many flowers were in bloom at that person's arrival time. This results in m iterations for each of the n persons. Therefore, the total number of operations is proportional to m*n, which gives a time complexity of O(m*n).

Space Complexity

O(1) – The brute force approach, as described, primarily iterates through the input 'flowers' and 'persons' arrays without creating any significant auxiliary data structures. The counter for each person's blooming flower count is a single integer variable. Therefore, the space used remains constant, independent of the size of the input arrays; thus, it has O(1) space complexity.

Optimal Solution

Approach

We want to efficiently count blooming flowers for different people's arrival times. The key is to organize the flower blooming and ending times so we can quickly find how many flowers are blooming when each person arrives using a binary search-like technique.

Here's how the algorithm would work step-by-step:

First, let's separate the start times and end times of each flower blooming period into two separate lists.
Then, sort both the start times list and the end times list in ascending order.
For each person's arrival time, use the sorted start times list to find out how many flowers have started blooming by that time. Think of this as finding the first flower that blooms *after* the person arrives, and subtracting 1 from that position to find out how many bloomed before or at the same time.
Next, use the sorted end times list to find out how many flowers have already stopped blooming by the time each person arrives. Similar to before, find the first flower that ends blooming *after* the person arrives, and use its position to tell how many have finished blooming.
Finally, subtract the number of flowers that have already stopped blooming from the number of flowers that have started blooming to find the number of flowers in full bloom when each person arrives. This gives us the final count for each person.

Code Implementation

def number_of_flowers_in_full_bloom(flowers, people):
    start_times = [flower[0] for flower in flowers]
    end_times = [flower[1] for flower in flowers]

    start_times.sort()
    end_times.sort()

    result = []

    for person_arrival_time in people:
        # Find num flowers blooming when the person arrives.
        started_blooming = find_index(start_times, person_arrival_time + 1)

        # Find num flowers that already stopped blooming.
        stopped_blooming = find_index(end_times, person_arrival_time + 1)

        result.append(started_blooming - stopped_blooming)

    return result

def find_index(flower_times, arrival_time):
    low = 0
    high = len(flower_times)

    while low < high:
        mid = (low + high) // 2

        if flower_times[mid] < arrival_time:
            low = mid + 1
        else:
            high = mid

    return low

Big(O) Analysis

Time Complexity

O(n log n) – The algorithm begins by separating start and end times of flowers into two lists of size n, where n is the number of flowers. Sorting each list takes O(n log n) time. For each person (let's say there are m people), we perform two binary searches on lists of size n, each taking O(log n) time. Therefore, searching for all m people takes O(m log n). Assuming m is proportional to n, the overall time complexity is dominated by the sorting step, giving us O(n log n).

Space Complexity

O(N) – The solution creates two new lists to store the start times and end times of the flowers. These lists will, in the worst case, contain all of the start and end times from the input, resulting in a total size of N, where N represents the number of flower blooming periods. Since the sorting is done in place (most likely timsort which has space O(n) or merge sort), it is not an auxiliary space. Therefore, the dominant factor in auxiliary space complexity is the two new lists that grow linearly with the number of flowers, making the overall space complexity O(N).

Edge Cases

Case	How to Handle
flowers is null or empty	Return an array of zeros with the same length as the people array.
people is null or empty	Return an empty array.
flowers array contains overlapping bloom ranges	The algorithm should correctly count flowers in bloom even if their ranges overlap.
A person arrives exactly at the start or end time of a flower's bloom	The problem statement clarifies inclusive ranges so the solution should include these times.
All flowers bloom at the exact same time	The algorithm should correctly count all blooming flowers for those arrival times.
The number of flowers or people is very large	Use an efficient algorithm like binary search to avoid exceeding time limits.
Flowers have very large bloom ranges, potentially leading to integer overflow if calculating durations	Avoid explicit duration calculations and rely on comparisons directly within the input range values.
People arrive at times outside any flower's bloom range	The corresponding entry in the answer array should be 0.