Rotate Image
MediumYou are given an n x n 2D matrix representing an image, rotate the image by 90 degrees (clockwise).
You have to rotate the image in-place, which means you have to modify the input 2D matrix directly. DO NOT allocate another 2D matrix and do the rotation.
Example 1:
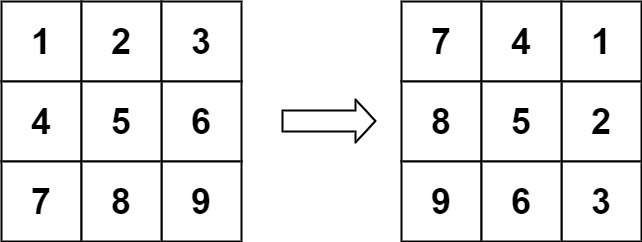
Input: matrix = [[1,2,3],[4,5,6],[7,8,9]] Output: [[7,4,1],[8,5,2],[9,6,3]]
Example 2:
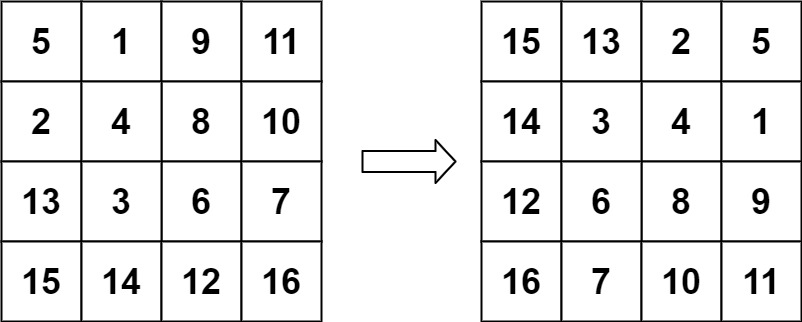
Input: matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]] Output: [[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]
Constraints:
n == matrix.length == matrix[i].length1 <= n <= 20-1000 <= matrix[i][j] <= 1000
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- Is the input matrix guaranteed to be a square matrix, meaning the number of rows equals the number of columns?
- What is the expected range of integer values within the matrix?
- Can I assume the matrix will always be valid and not null or empty?
- If the matrix is a 1x1 matrix, should it remain unchanged?
- Are we optimizing for space complexity (in-place modification is a must) and time complexity?
Brute Force Solution
Approach
Imagine you're physically rotating a square picture frame by 90 degrees. The brute force way is to take each pixel in the original frame and individually move it to its new location in the rotated frame. This involves going through every pixel one by one and placing it correctly in the new frame.
Here's how the algorithm would work step-by-step:
- Create a completely new empty picture frame that has the same size as the original.
- Look at the very first pixel in the original picture frame.
- Figure out where that pixel should end up in the rotated picture frame.
- Copy the color of the pixel from the original frame to its new spot in the rotated frame.
- Move on to the next pixel in the original picture frame and repeat the process: figure out its new location and copy its color.
- Keep doing this for every single pixel in the original picture frame, always finding its new location and copying its color to the new picture frame.
- Once you've gone through all the pixels in the original frame, the new picture frame will contain the fully rotated image.
Code Implementation
def rotate_image_brute_force(matrix):
matrix_size = len(matrix)
# Create a new matrix to store the rotated image
rotated_matrix = [[0] * matrix_size for _ in range(matrix_size)]
for row_index in range(matrix_size):
for column_index in range(matrix_size):
# Calculate the new position for the pixel after rotation.
new_row_index = column_index
new_column_index = matrix_size - 1 - row_index
# Copy the pixel to its new location in the rotated matrix.
rotated_matrix[new_row_index][new_column_index] = matrix[row_index][column_index]
# Update the original matrix with the rotated image.
for row_index in range(matrix_size):
for column_index in range(matrix_size):
# Copy rotated matrix back to the original. Required by prompt.
matrix[row_index][column_index] = rotated_matrix[row_index][column_index]
# The problem asks for in-place rotation, so return is technically not needed.
return matrixBig(O) Analysis
Optimal Solution
Approach
To rotate the image efficiently, we don't move each pixel individually. Instead, we perform a two-step process: first flip the image horizontally, and then flip it along the diagonal. This achieves the 90-degree clockwise rotation in place.
Here's how the algorithm would work step-by-step:
- First, imagine flipping the image from left to right, like looking at a reflection in a mirror.
- Next, swap elements across the diagonal, meaning the element in the top-left corner stays put, but the element to its right swaps with the element below it, and so on.
- By doing these two flips in sequence, the image is rotated 90 degrees clockwise.
Code Implementation
def rotate_image(matrix):
matrix_size = len(matrix)
# Flip horizontally to prepare for the diagonal swap.
for row in matrix:
row.reverse()
# Swap across the main diagonal.
for row_index in range(matrix_size):
for column_index in range(row_index + 1, matrix_size):
# Transpose elements
matrix[row_index][column_index], matrix[column_index][row_index] = \
matrix[column_index][row_index], matrix[row_index][column_index]
# The image is now rotated 90 degrees clockwise in place.
return matrix
Big(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Null or empty matrix | Return immediately without modification if the matrix is null or has zero rows or columns. |
| 1x1 matrix | No rotation is needed for a 1x1 matrix, so return immediately without modification. |
| 2x2 matrix | The algorithm should correctly rotate the elements within the 2x2 matrix. |
| Large matrix (e.g., 1000x1000) | Ensure the algorithm's time and space complexity are efficient enough to handle large matrices without exceeding memory limits or causing timeouts (ideally O(n^2) time and O(1) space). |
| Matrix with negative numbers, zeros, and positive numbers | The algorithm should correctly rotate the matrix regardless of the values of the elements, including negative numbers, zeros, and positive numbers. |
| Non-square matrix | The problem description explicitly states it's a square matrix; however, in a real interview clarifying this constraint is important; if it is not square, throw an exception or return an error code. |
| Matrix with extreme values (e.g., Integer.MAX_VALUE, Integer.MIN_VALUE) | The algorithm should handle extreme integer values without causing integer overflow issues during the rotation process. |
| Matrix filled with identical values | The algorithm should function correctly even if all the values in the matrix are the same. |