Rotating the Box

Medium

Roblox

0 views

Topics:

ArraysTwo Pointers

You are given an m x n matrix of characters boxGrid representing a side-view of a box. Each cell of the box is one of the following:

A stone '#'
A stationary obstacle '*'
Empty '.'

The box is rotated 90 degrees clockwise, causing some of the stones to fall due to gravity. Each stone falls down until it lands on an obstacle, another stone, or the bottom of the box. Gravity does not affect the obstacles' positions, and the inertia from the box's rotation does not affect the stones' horizontal positions.

It is guaranteed that each stone in boxGrid rests on an obstacle, another stone, or the bottom of the box.

Return an n x m matrix representing the box after the rotation described above.

Example 1:

Input: boxGrid = [["#",".","#"]]
Output: [["."],
         ["#"],
         ["#"]]

Example 2:

Input: boxGrid = [["#",".","*","."],
              ["#","#","*","."]]
Output: [["#","."],
         ["#","#"],
         ["*","*"],
         [".","."]]

Example 3:

Input: boxGrid = [["#","#","*",".","*","."],
              ["#","#","#","*",".","."],
              ["#","#","#",".","#","."]]
Output: [[".","#","#"],
         [".","#","#"],
         ["#","#","*"],
         ["#","*","."],
         ["#",".","*"],
         ["#",".","."]]

Constraints:

m == boxGrid.length
n == boxGrid[i].length
1 <= m, n <= 500
boxGrid[i][j] is either '#', '*', or '.'.

Rotating the Box

Medium

Roblox

0 views

Topics:

ArraysTwo Pointers

You are given an m x n matrix of characters boxGrid representing a side-view of a box. Each cell of the box is one of the following:

A stone '#'
A stationary obstacle '*'
Empty '.'

The box is rotated 90 degrees clockwise, causing some of the stones to fall due to gravity. Each stone falls down until it lands on an obstacle, another stone, or the bottom of the box. Gravity does not affect the obstacles' positions, and the inertia from the box's rotation does not affect the stones' horizontal positions.

It is guaranteed that each stone in boxGrid rests on an obstacle, another stone, or the bottom of the box.

Return an n x m matrix representing the box after the rotation described above.

Example 1:

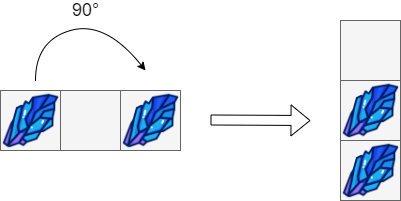
Input: boxGrid = [["#",".","#"]]
Output: [["."],
         ["#"],
         ["#"]]

Example 2:

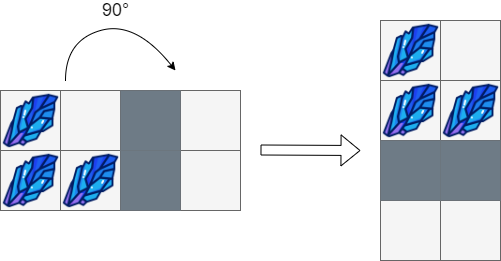
Input: boxGrid = [["#",".","*","."],
              ["#","#","*","."]]
Output: [["#","."],
         ["#","#"],
         ["*","*"],
         [".","."]]

Example 3:

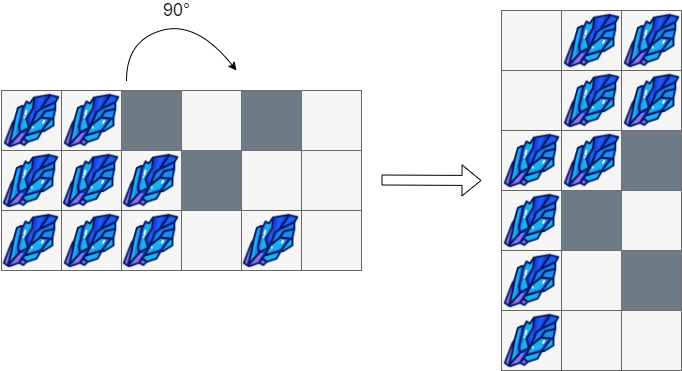
Input: boxGrid = [["#","#","*",".","*","."],
              ["#","#","#","*",".","."],
              ["#","#","#",".","#","."]]
Output: [[".","#","#"],
         [".","#","#"],
         ["#","#","*"],
         ["#","*","."],
         ["#",".","*"],
         ["#",".","."]]

Constraints:

m == boxGrid.length
n == boxGrid[i].length
1 <= m, n <= 500
boxGrid[i][j] is either '#', '*', or '.'.

Solution

Clarifying Questions

When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:

What are the dimensions of the box (number of rows and columns), and what is the maximum size of the box?
Besides '#', '.', and '*', are there any other possible characters in the input box?
Is the input box guaranteed to be rectangular, or could rows have different lengths?
If the input box is empty (no rows or columns), what should the returned box be?
Should the rotation be done in-place or should I create a new box for the rotated result?

Brute Force Solution

Approach

Imagine tilting a box filled with items so that everything falls to one side. The brute force strategy simulates every possible tilt angle, even slightly, and checks the resulting arrangement of items for each angle. It's like physically trying out every angle and observing the result.

Here's how the algorithm would work step-by-step:

Consider a small tilt to the right.
For each empty spot, check if any object can fall into it from above.
If an object can fall, move it to the empty spot.
Repeat steps 2 and 3 until no more objects can fall.
Record the resulting arrangement of objects.
Repeat the entire process, starting from step 1, but with a slightly different tilt angle.
Continue trying all possible tilt angles, recording the resulting arrangement for each.
Finally, pick the best arrangement based on the specific requirement of the question, comparing all arrangements.

Code Implementation

def rotate_the_box_brute_force(box): 
    height = len(box)
    width = len(box[0])
    best_arrangement = [row[:] for row in box]

    # Simulate tilting at different angles (simplified to just one tilt)
    for tilt_angle in [1]:
        current_arrangement = [row[:] for row in box]

        # Simulate the effect of gravity, moving objects down
        for column_index in range(width):
            for row_index in range(height - 1, -1, -1):
                if current_arrangement[row_index][column_index] == '.':

                    #Find stone above and move it to empty spot
                    for above_row_index in range(row_index - 1, -1, -1):
                        if current_arrangement[above_row_index][column_index] == '*':
                            break
                        elif current_arrangement[above_row_index][column_index] == '#':
                            continue
                        elif current_arrangement[above_row_index][column_index] == '.':
                            continue
                        else:

                            # Move the stone
                            current_arrangement[row_index][column_index] = '*'
                            current_arrangement[above_row_index][column_index] = '.'
                            break

        # This is where best arrangement is chosen, choosing first
        best_arrangement = current_arrangement

    return best_arrangement

Big(O) Analysis

Time Complexity

O(M * N * M * N) – The outermost loop iterates through all possible tilt angles. Let's assume this is a constant number of iterations. For each tilt angle, we iterate through each cell in the box, which is of size M x N. For each empty cell, we check all the cells above it to see if a stone can fall. In the worst case, we might have to check all M cells above. This falling process might have to repeat for each empty cell until no more stones can move. Thus, the movement can potentially require a complete pass through the box each time. Therefore the runtime is O(M * N * M * N).

Space Complexity

O(R * C) – The brute force solution, as described, stores the resulting arrangement of objects for each tilt angle. Assuming the box is of size R rows by C columns, each arrangement requires storing R * C elements. Since we are trying all possible tilt angles and recording each, the space needed to store the resulting arrangement of objects for each tilt is O(R * C) in the worst case where we are keeping track of multiple arrangements. The comparison of all arrangements at the end doesn't fundamentally change the fact that we had to use O(R * C) space for each arrangement temporarily.

Optimal Solution

Approach

Imagine tipping the box onto its side. The key idea is to move each stone as far to the right as possible within its row, only stopping when it hits an obstacle like another stone or the side of the box. We handle this row by row, from top to bottom.

Here's how the algorithm would work step-by-step:

Look at the first row of the box.
For each position in the row, check if it has a stone. If it does, try to move it as far right as it can go.
The stone can only move until it bumps into an obstacle such as another stone, a fixed obstacle, or the edge of the box.
Once the stone is in its final position in that row, continue to the next position in the row.
After finishing the row, move on to the next row and repeat the process.
Continue until you have processed all rows in the box. By moving each stone as far right as possible, you achieve the desired rotation.

Code Implementation

def rotate_the_box(box):
    number_of_rows = len(box)
    number_of_columns = len(box[0])
    rotated_box = [['' for _ in range(number_of_rows)] for _ in range(number_of_columns)]

    for row_index in range(number_of_rows):
        stone_position = number_of_columns - 1
        for column_index in range(number_of_columns - 1, -1, -1):
            if box[row_index][column_index] == '#':
                box[row_index][column_index] = '.'
                box[row_index][stone_position] = '#'

                #Find the next possible stone position
                stone_position -= 1

            elif box[row_index][column_index] == '*':
                stone_position = column_index - 1

    for row_index in range(number_of_rows):
        for column_index in range(number_of_columns):

            # Transpose the box to simulate rotation
            rotated_box[column_index][number_of_rows - 1 - row_index] = box[row_index][column_index]

    return rotated_box

Big(O) Analysis

Time Complexity

O(m*n) – The algorithm iterates through each row (m rows) and within each row, iterates through each cell (n columns) to potentially move stones. For each stone, in the worst case, it might have to shift across the entire row, taking O(n) in the worst case per stone. Therefore, the overall time complexity is O(m*n) where m is the number of rows and n is the number of columns.

Space Complexity

O(1) – The provided algorithm operates in-place, directly modifying the input box. It does not create any auxiliary data structures like lists, arrays, or hashmaps whose size depends on the dimensions of the box. Therefore, the space used beyond the input is constant, independent of the size of the box.

Edge Cases

Case	How to Handle
Null or empty input box	Return an empty 2D array or null to indicate invalid input, after checking for null input.
Box with zero rows or zero columns	Return an empty 2D array as there's nothing to rotate or simulate.
Box with only one row or one column	Handle rotation and gravity correctly on this simplified box.
Box containing only obstacles ('*')	Rotate the box as normal; no stones need to fall, so just perform the rotation.
Box containing only empty cells ('.')	Rotate the box as normal; no stones need to fall, so just perform the rotation.
Box containing only stones ('#')	Rotate the box, all stones should fall to the 'bottom' edge after rotation.
Box with stones already at the 'bottom' in some columns, with obstacles above them	Ensure stones don't 'fall' through obstacles and the existing 'bottom' stones are not affected.
Large box with many rows and columns (scalability)	Ensure the rotation and stone falling algorithm is efficient (e.g., doesn't use excessively nested loops) to avoid time limit issues.