Binary Tree Preorder Traversal
EasyGiven the root of a binary tree, return the preorder traversal of its nodes' values.
Example 1:
Input: root = [1,null,2,3]
Output: [1,2,3]
Explanation:
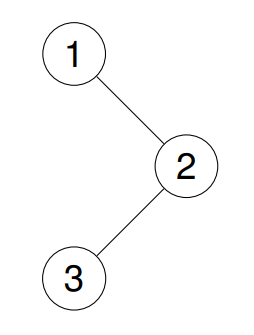
Example 2:
Input: root = [1,2,3,4,5,null,8,null,null,6,7,9]
Output: [1,2,4,5,6,7,3,8,9]
Explanation:
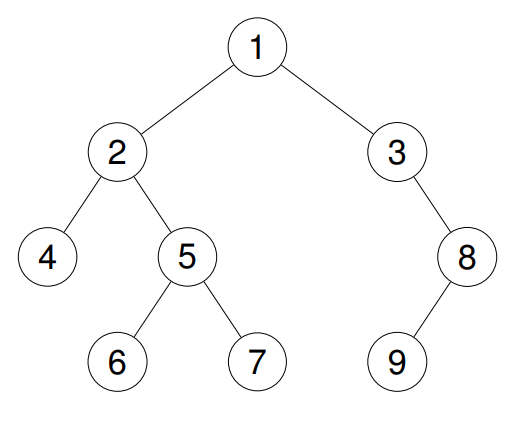
Example 3:
Input: root = []
Output: []
Example 4:
Input: root = [1]
Output: [1]
Constraints:
- The number of nodes in the tree is in the range
[0, 100]. -100 <= Node.val <= 100
Follow up: Recursive solution is trivial, could you do it iteratively?
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- Can the binary tree be empty (i.e., `root` is null)? If so, what should I return?
- What is the range of values that the nodes in the binary tree can have?
- Is the binary tree guaranteed to be a valid binary tree, or should I handle potential invalid tree structures?
- Are there any memory constraints on the size of the output list I should be aware of?
- Can the tree be extremely skewed (e.g., a linked list-like structure) potentially impacting the call stack depth?
Brute Force Solution
Approach
The brute force approach to traversing a binary tree in preorder is like meticulously visiting every node in the tree in a specific order. We visit the current node first, then its left child, and finally its right child. This is done recursively, ensuring that we explore all possibilities to get the correct traversal sequence.
Here's how the algorithm would work step-by-step:
- First, go to the very top node of the tree and record its value.
- Next, go to the node on the left side of that top node, if there is one, and record its value.
- From that left node, if it has its own left node, go there and record that value.
- Keep going down the left side of the tree, recording values as you go, until you reach a node that has no left node.
- When you can't go left anymore, go to the right node of the current node, if there is one, and record its value.
- Now repeat the process starting at that right node: go as far left as possible, recording each value, then go right.
- Once you have visited and recorded the value of every node in the tree, in this specific order, you're done.
Code Implementation
def preorder_traversal_brute_force(root):
result_list = []
def traverse_tree(node):
if not node:
return
# Visit the current node and record its value.
result_list.append(node.val)
# Recursively traverse the left subtree.
traverse_tree(node.left)
# Recursively traverse the right subtree.
traverse_tree(node.right)
traverse_tree(root)
return result_listBig(O) Analysis
Optimal Solution
Approach
We need to visit the root of a tree, then the left side, then the right side. The most efficient way to do this uses the computer's memory to keep track of where we need to go next as we walk through the tree.
Here's how the algorithm would work step-by-step:
- Start at the very top (the root) of the tree.
- Record the value of the current node (the one you are visiting) as part of the result.
- If there's a left branch from where you are, remember where you are and then go down the left branch.
- Repeat the 'record value' and 'go left' steps as much as you can until you can't go left anymore.
- If you can't go left, check if you can go right from where you last were. If so, go right.
- Keep repeating the process of going left, then right until you have visited every node in the tree. The stored list of values is your final result.
Code Implementation
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
def preorder_traversal(root):
result_list = []
node_stack = []
current_node = root
while current_node or node_stack:
# Traverse left as far as possible and record the values
while current_node:
result_list.append(current_node.val)
# Store current node to potentially revisit it later
node_stack.append(current_node)
current_node = current_node.left
# Backtrack and go right
current_node = node_stack.pop()
# If there's a right child, explore it
if current_node.right:
current_node = current_node.right
else:
current_node = None
return result_listBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Null root node | Return an empty list when the root is null, as there's nothing to traverse. |
| Tree with only a root node | Return a list containing only the root's value, since that's the entire traversal. |
| Completely skewed tree (left or right) | Recursive solution's call stack will grow linearly with tree height, potentially leading to stack overflow for extremely deep trees; iterative solutions can avoid this. |
| Large tree (potential memory limitations) | Iterative solutions might be preferable to recursive solutions to avoid excessive stack usage for very large trees which could exhaust memory resources. |
| Tree with duplicate values | Duplicate node values don't affect the preorder traversal algorithm's correctness, so it functions as intended. |
| Tree with negative or zero node values | Negative or zero values are valid node values and should be treated the same as any other integer value. |
| Integer overflow in node values (if applicable) | If node values can exceed the maximum integer value, consider using a larger data type or employing modular arithmetic if appropriate to prevent integer overflows. |
| Recursive solution exceeds maximum recursion depth | For very deep trees, the recursive solution may hit the maximum recursion depth, so an iterative solution using a stack is a good alternative. |