Maximum Height by Stacking Cuboids

Hard

Samsung

1 view

Topics:

ArraysDynamic Programming

Given n cuboids where the dimensions of the i^th cuboid is cuboids[i] = [width_i, length_i, height_i] (0-indexed). Choose a subset of cuboids and place them on each other.

You can place cuboid i on cuboid j if width_i <= width_j and length_i <= length_j and height_i <= height_j. You can rearrange any cuboid's dimensions by rotating it to put it on another cuboid.

Return the maximum height of the stacked cuboids.

Example 1:

Input: cuboids = [[50,45,20],[95,37,53],[45,23,12]]
Output: 190
Explanation:
Cuboid 1 is placed on the bottom with the 53x37 side facing down with height 95.
Cuboid 0 is placed next with the 45x20 side facing down with height 50.
Cuboid 2 is placed next with the 23x12 side facing down with height 45.
The total height is 95 + 50 + 45 = 190.

Example 2:

Input: cuboids = [[38,25,45],[76,35,3]]
Output: 76
Explanation:
You can't place any of the cuboids on the other.
We choose cuboid 1 and rotate it so that the 35x3 side is facing down and its height is 76.

Example 3:

Input: cuboids = [[7,11,17],[7,17,11],[11,7,17],[11,17,7],[17,7,11],[17,11,7]]
Output: 102
Explanation:
After rearranging the cuboids, you can see that all cuboids have the same dimension.
You can place the 11x7 side down on all cuboids so their heights are 17.
The maximum height of stacked cuboids is 6 * 17 = 102.

Constraints:

n == cuboids.length
1 <= n <= 100
1 <= width_i, length_i, height_i <= 100

Maximum Height by Stacking Cuboids

Hard

Samsung

1 view

Topics:

ArraysDynamic Programming

Given n cuboids where the dimensions of the i^th cuboid is cuboids[i] = [width_i, length_i, height_i] (0-indexed). Choose a subset of cuboids and place them on each other.

You can place cuboid i on cuboid j if width_i <= width_j and length_i <= length_j and height_i <= height_j. You can rearrange any cuboid's dimensions by rotating it to put it on another cuboid.

Return the maximum height of the stacked cuboids.

Example 1:

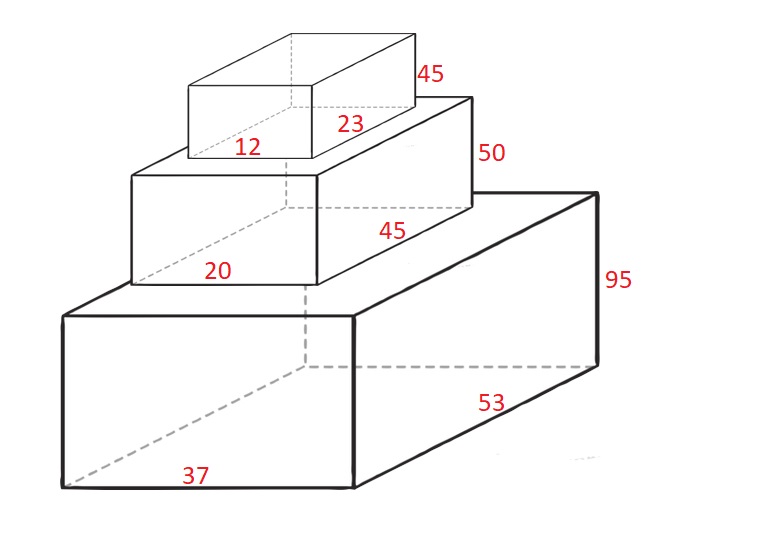
Input: cuboids = [[50,45,20],[95,37,53],[45,23,12]]
Output: 190
Explanation:
Cuboid 1 is placed on the bottom with the 53x37 side facing down with height 95.
Cuboid 0 is placed next with the 45x20 side facing down with height 50.
Cuboid 2 is placed next with the 23x12 side facing down with height 45.
The total height is 95 + 50 + 45 = 190.

Example 2:

Input: cuboids = [[38,25,45],[76,35,3]]
Output: 76
Explanation:
You can't place any of the cuboids on the other.
We choose cuboid 1 and rotate it so that the 35x3 side is facing down and its height is 76.

Example 3:

Input: cuboids = [[7,11,17],[7,17,11],[11,7,17],[11,17,7],[17,7,11],[17,11,7]]
Output: 102
Explanation:
After rearranging the cuboids, you can see that all cuboids have the same dimension.
You can place the 11x7 side down on all cuboids so their heights are 17.
The maximum height of stacked cuboids is 6 * 17 = 102.

Constraints:

n == cuboids.length
1 <= n <= 100
1 <= width_i, length_i, height_i <= 100

Solution

Clarifying Questions

When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:

What are the dimensions of the cuboids represented by the input array? Are they integers, and are they guaranteed to be positive?
What is the maximum number of cuboids I should expect in the input array?
If no stacking arrangement is possible, what value should I return?
Can cuboids be rotated to achieve a higher stack? If so, is there a cost associated with rotating a cuboid?
If multiple stacking arrangements result in the same maximum height, is any one of them acceptable?

Brute Force Solution

Approach

Imagine you're trying to build the tallest tower possible with a set of blocks. The brute force method means we try every single possible combination of stacking the blocks to see which one results in the highest tower. This involves exploring all the different orders and orientations in which we can place the blocks.

Here's how the algorithm would work step-by-step:

First, consider each block as a potential base of the tower.
For each chosen base block, try placing every other block on top of it, but only if the block below is bigger or equal in all dimensions.
Keep going by trying to add another block on top of the second block, again making sure it is not bigger in any dimension than the block below.
Continue stacking blocks as long as you can find blocks that fit and haven't been used yet in that particular stack.
Keep track of the height of each possible tower you build this way.
Once you've tried all possible combinations of blocks and their arrangements, choose the tallest tower from all the ones you built.

Code Implementation

def max_height_by_stacking_cuboids_brute_force(cuboids):
    max_tower_height = 0
    number_of_cuboids = len(cuboids)

    for i in range(number_of_cuboids):
        # Consider each cuboid as the base
        for rotation in get_rotations(cuboids[i]):
            current_tower_height = rotation[2]
            current_stack = [rotation]
            unused_cuboids = list(range(number_of_cuboids))
            unused_cuboids.remove(i)
            max_tower_height = max(max_tower_height, 
                                  build_tower(
                                      current_stack, 
                                      unused_cuboids, 
                                      cuboids, 
                                      current_tower_height
                                  ))

    return max_tower_height

def build_tower(current_stack, unused_cuboids, cuboids, current_tower_height):
    max_height = current_tower_height
    if not unused_cuboids:
        return max_height

    for cuboid_index in unused_cuboids:
        # Try to place cuboid on top of current stack
        for rotation in get_rotations(cuboids[cuboid_index]):
            if can_place(rotation, current_stack[-1]):
                # If the cuboid can be placed, add it to the stack
                new_stack = current_stack + [rotation]
                new_unused_cuboids = list(unused_cuboids)
                new_unused_cuboids.remove(cuboid_index)
                new_tower_height = current_tower_height + rotation[2]
                
                # Recursively build the tower further
                max_height = max(max_height, 
                                 build_tower(
                                     new_stack, 
                                     new_unused_cuboids, 
                                     cuboids, 
                                     new_tower_height
                                 ))
    
    return max_height

def get_rotations(cuboid):
    rotations = []
    rotations.append(tuple(sorted(cuboid)))
    
    return rotations

def can_place(top_cuboid, bottom_cuboid):
    # Check if all dimensions of top are <= bottom
    return all(top_cuboid[i] <= bottom_cuboid[i] for i in range(3))

Try it yourself on LeetCode

Big(O) Analysis

Time Complexity

O(n!) – The provided approach attempts all possible stacking combinations and orientations of n cuboids. In the worst case, we explore all permutations of the cuboids, which involves n! possibilities. For each permutation, we might need to check each cuboid to determine if it can be placed on top of the existing stack, involving further comparisons. Consequently, the dominant factor is the exploration of all permutations, resulting in a time complexity of O(n!).

Space Complexity

O(N) – The brute force approach, as described, explores all possible stack combinations. In the worst-case scenario, to keep track of the blocks already used in a particular stack, we might need a boolean array of size N (where N is the number of cuboids) for each potential stack starting from any cuboid. Although not explicitly stated in the problem, the height of the stack is tracked. However, the dominant auxiliary space complexity stems from the need to mark used cuboids in each recursion branch. Therefore, the auxiliary space complexity is O(N).

Optimal Solution

Approach

To find the maximum height of stacked cuboids, we need to cleverly arrange them so that taller cuboids are always below smaller ones. This approach involves first organizing each cuboid's dimensions and then sorting all cuboids to build the tallest possible stack from the bottom up.

Here's how the algorithm would work step-by-step:

For each cuboid, make sure its sides are in increasing order, so we can easily compare them.
Sort all the cuboids based on their dimensions, prioritizing the largest cuboids to be at the bottom.
Start building the stack from the bottom. At each step, consider if you can place the current cuboid on top of the previous one. A cuboid can be placed only if all its dimensions are less than or equal to the dimensions of the cuboid below it.
If a cuboid can be placed, add its height to the current stack height. Otherwise, skip it and try the next one.
Keep track of the maximum stack height you've found so far. After considering all cuboids, the maximum height will be your answer.

Code Implementation

def max_height(cuboids):
    for cuboid in cuboids:
        cuboid.sort()

    # Sort cuboids to prioritize larger bases.
    cuboids.sort(key=lambda x: (x[0], x[1], x[2]), reverse=True)

    number_of_cuboids = len(cuboids)
    maximum_heights = [0] * number_of_cuboids

    for i in range(number_of_cuboids):
        maximum_heights[i] = cuboids[i][2]

        # Find the maximum height by including current cuboid.
        for j in range(i):
            if cuboids[j][0] >= cuboids[i][0] and \
               cuboids[j][1] >= cuboids[i][1] and \
               cuboids[j][2] >= cuboids[i][2]:

                maximum_heights[i] = max(maximum_heights[i], maximum_heights[j] + cuboids[i][2])

    # Find the overall maximum height.
    maximum_overall_height = 0
    for height in maximum_heights:
        maximum_overall_height = max(maximum_overall_height, height)

    return maximum_overall_height

Try it yourself on LeetCode

Big(O) Analysis

Time Complexity

O(n^2) – The algorithm first sorts each of the n cuboids' dimensions which takes O(1) time per cuboid since there are only three dimensions, leading to O(n) for all cuboids. Then the algorithm sorts the n cuboids, costing O(n log n). After sorting, it iterates through the cuboids to build the maximum height stack. For each cuboid, it compares it with all the preceding cuboids to find the best possible stack height, resulting in a nested loop structure. This comparison takes O(n) time for each of the n cuboids. Thus, the dominant operation is the nested loop comparison that takes approximately n * n/2 operations, which simplifies to O(n^2).

Space Complexity

O(N) – The algorithm sorts the input cuboids array in place, but the crucial auxiliary space comes from the dynamic programming approach used implicitly when building the stack. This approach requires storing intermediate maximum heights for each cuboid, which is achieved through the inherent recursion stack. The depth of the recursion stack depends on the number of cuboids (N), where N is the number of cuboids given as input. Therefore, the space complexity is proportional to N.

Edge Cases

Case	How to Handle
Empty input cuboids array	Return 0 if the input array is empty, as no height can be formed.
Single cuboid input	Return the height of the single cuboid if the input only contains one cuboid, as it's already the maximum possible height.
Cuboids with dimensions of zero	Filter out any cuboids with any dimension being zero, as they cannot contribute to the height.
Large number of cuboids	The dynamic programming approach should scale reasonably, but consider potential memory limitations for very large inputs and optimize accordingly.
Cuboids with identical dimensions	The algorithm should correctly handle identical cuboids by considering all valid stacking permutations, potentially using memoization to avoid redundant calculations.
Integer overflow when summing heights	Use a data type that can accommodate large sums of heights (e.g., long) to prevent integer overflow.
No valid stacking order exists	The algorithm should return 0 if no cuboid can be stacked on top of another according to the problem constraints.
Cuboid dimensions are very large integers	Ensure that comparisons between cuboid dimensions don't result in integer overflow or unexpected behavior by using appropriate data types (e.g., long).