Minimum Area Rectangle
MediumYou are given an array of points in the X-Y plane points where points[i] = [xi, yi].
Return the minimum area of a rectangle formed from these points, with sides parallel to the X and Y axes. If there is not any such rectangle, return 0.
Example 1:
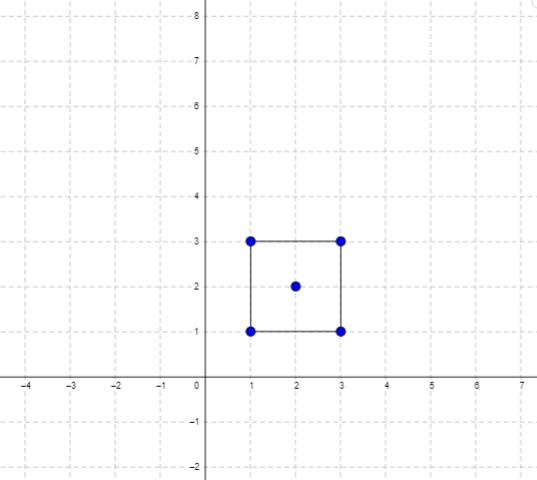
Input: points = [[1,1],[1,3],[3,1],[3,3],[2,2]] Output: 4
Example 2:
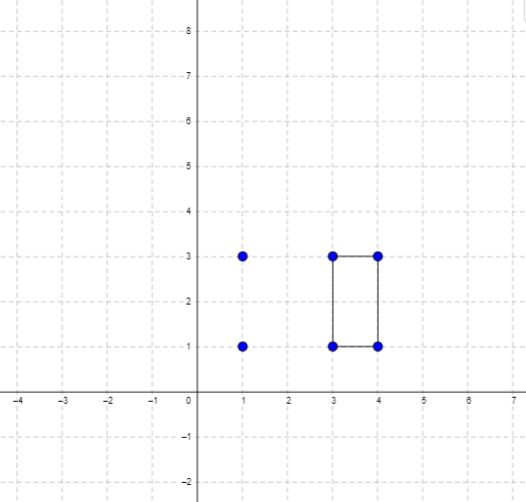
Input: points = [[1,1],[1,3],[3,1],[3,3],[4,1],[4,3]] Output: 2
Constraints:
1 <= points.length <= 500points[i].length == 20 <= xi, yi <= 4 * 104- All the given points are unique.
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What is the data type of the coordinates of the points? Are they integers or floating-point numbers?
- Is it possible for the input to contain fewer than 4 points? If so, what should I return?
- If no rectangle can be formed from the given points, what should the function return (e.g., 0, null, -1)?
- Can there be duplicate points in the input? If so, how should they be handled?
- If there are multiple rectangles with the same minimum area, is any one of them acceptable, or is there a specific rectangle I should return based on some criteria (e.g., lexicographically smallest coordinates)?
Brute Force Solution
Approach
The brute force method for finding the minimum area rectangle involves checking every possible combination of points to see if they form a rectangle. We exhaustively examine each set of four points and determine if they could be the corners of a rectangle.
Here's how the algorithm would work step-by-step:
- Take any four points from the given collection of points.
- Check if those four points form a rectangle. To do this, verify if the sides are parallel to the x and y axes and if the opposite sides are equal in length, indicating a valid rectangle.
- If the four points do form a rectangle, calculate its area.
- Compare the calculated area with the smallest area found so far. If the new area is smaller, update the smallest area.
- Repeat this process for every possible combination of four points from the original set.
- After checking all possible combinations, the smallest area recorded is the minimum area of a rectangle that can be formed from the given points.
Code Implementation
def minimum_area_rectangle_brute_force(points):
minimum_area = float('inf')
number_of_points = len(points)
for first_point_index in range(number_of_points):
for second_point_index in range(first_point_index + 1, number_of_points):
for third_point_index in range(second_point_index + 1, number_of_points):
for fourth_point_index in range(third_point_index + 1, number_of_points):
first_point = points[first_point_index]
second_point = points[second_point_index]
third_point = points[third_point_index]
fourth_point = points[fourth_point_index]
# Check if the four points form a rectangle
if is_rectangle(first_point, second_point, third_point, fourth_point):
#Calculate the area of the rectangle
area = calculate_rectangle_area(first_point, second_point, third_point, fourth_point)
#Update the minimum area if the current area is smaller
minimum_area = min(minimum_area, area)
if minimum_area == float('inf'):
return 0
else:
return minimum_area
def is_rectangle(first_point, second_point, third_point, fourth_point):
# Check if sides are parallel to x and y axes and opposite sides are equal
x_values = [first_point[0], second_point[0], third_point[0], fourth_point[0]]
y_values = [first_point[1], second_point[1], third_point[1], fourth_point[1]]
x_values.sort()
y_values.sort()
if x_values[0] == x_values[1] and x_values[2] == x_values[3] and y_values[0] == y_values[1] and y_values[2] == y_values[3]:
possible_corners = [(x_values[0], y_values[0]), (x_values[2], y_values[0]), (x_values[2], y_values[2]), (x_values[0], y_values[2])]
points_set = set(tuple(point) for point in [first_point, second_point, third_point, fourth_point])
if all(corner in points_set for corner in possible_corners):
return True
return False
def calculate_rectangle_area(first_point, second_point, third_point, fourth_point):
#Calculate the length of sides using distance formula
x_values = [first_point[0], second_point[0], third_point[0], fourth_point[0]]
y_values = [first_point[1], second_point[1], third_point[1], fourth_point[1]]
x_values.sort()
y_values.sort()
width = x_values[2] - x_values[0]
height = y_values[2] - y_values[0]
return width * heightBig(O) Analysis
Optimal Solution
Approach
The key to efficiently finding the minimum area rectangle is to focus on finding pairs of points that could form a diagonal. We use the points to look for potential rectangle corners and calculate areas only for valid rectangles.
Here's how the algorithm would work step-by-step:
- First, store all the given points in a way that lets you quickly check if a point exists.
- Now, take each pair of points and imagine they form a diagonal of a potential rectangle.
- For each potential diagonal, check if the other two points needed to form a rectangle exist in your stored points. These points would complete the rectangle using the initial diagonal.
- If the other two points exist, you've found a rectangle! Calculate its area.
- Keep track of the smallest area you've found so far.
- After checking all possible diagonals, if you found any rectangles, return the smallest area; otherwise, if no rectangle was found, indicate that.
Code Implementation
def minimum_area_rectangle(points):
minimum_area = float('inf')
point_set = set((x, y) for x, y in points)
for i in range(len(points)):
for j in range(i + 1, len(points)):
point_one_x, point_one_y = points[i]
point_two_x, point_two_y = points[j]
# Ensure diagonal is not a line
if point_one_x == point_two_x or point_one_y == point_two_y:
continue
# Find the other two points
other_point_one_x = point_one_x
other_point_one_y = point_two_y
other_point_two_x = point_two_x
other_point_two_y = point_one_y
# Check if the other two points exist
if (other_point_one_x, other_point_one_y) in point_set and \
(other_point_two_x, other_point_two_y) in point_set:
# We found a rectangle, calculate area
area = abs(point_one_x - point_two_x) * abs(point_one_y - point_two_y)
# Update minimum area
minimum_area = min(minimum_area, area)
# No rectangle found
if minimum_area == float('inf'):
return 0
# Return the minimum area
else:
return minimum_areaBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Null or empty input list of points | Return 0 immediately, as no rectangle can be formed without points. |
| Input list contains fewer than 4 points | Return 0, as at least 4 points are needed to form a rectangle. |
| Input list contains points that are not integers or are malformed | Validate input to only process valid points and throw exception/return error for invalid input. |
| The input list contains duplicate points | Using a set to store points will eliminate duplicates which will not affect the minimum area. |
| No rectangle can be formed from the given points | Return 0 after iterating through all possible combinations of points. |
| Integer overflow when calculating area | Use a data type with a larger range, such as long, to store the area to prevent overflow. |
| Points form a square instead of a rectangle | The area calculation will correctly compute the area of a square, which is a special case of a rectangle. |
| Input contains very large coordinates, potentially causing memory issues or slow computations | Consider the memory implications of storing large coordinate values, and optimize data structures/algorithms where possible. |