Game of Life

Medium

Two Sigma

1 view

Topics:

Arrays

According to Wikipedia's article: "The Game of Life, also known simply as Life, is a cellular automaton devised by the British mathematician John Horton Conway in 1970."

The board is made up of an m x n grid of cells, where each cell has an initial state: live (represented by a 1) or dead (represented by a 0). Each cell interacts with its eight neighbors (horizontal, vertical, diagonal) using the following four rules (taken from the above Wikipedia article):

Any live cell with fewer than two live neighbors dies as if caused by under-population.
Any live cell with two or three live neighbors lives on to the next generation.
Any live cell with more than three live neighbors dies, as if by over-population.
Any dead cell with exactly three live neighbors becomes a live cell, as if by reproduction.

The next state of the board is determined by applying the above rules simultaneously to every cell in the current state of the m x n grid board. In this process, births and deaths occur simultaneously.

Given the current state of the board, update the board to reflect its next state.

Note that you do not need to return anything.

Example 1:

Input: board = [[0,1,0],[0,0,1],[1,1,1],[0,0,0]]
Output: [[0,0,0],[1,0,1],[0,1,1],[0,1,0]]

Example 2:

Input: board = [[1,1],[1,0]]
Output: [[1,1],[1,1]]

Constraints:

m == board.length
n == board[i].length
1 <= m, n <= 25
board[i][j] is 0 or 1.

Follow up:

Could you solve it in-place? Remember that the board needs to be updated simultaneously: You cannot update some cells first and then use their updated values to update other cells.
In this question, we represent the board using a 2D array. In principle, the board is infinite, which would cause problems when the active area encroaches upon the border of the array (i.e., live cells reach the border). How would you address these problems?

Game of Life

Medium

Two Sigma

1 view

Topics:

Arrays

According to Wikipedia's article: "The Game of Life, also known simply as Life, is a cellular automaton devised by the British mathematician John Horton Conway in 1970."

The board is made up of an m x n grid of cells, where each cell has an initial state: live (represented by a 1) or dead (represented by a 0). Each cell interacts with its eight neighbors (horizontal, vertical, diagonal) using the following four rules (taken from the above Wikipedia article):

Any live cell with fewer than two live neighbors dies as if caused by under-population.
Any live cell with two or three live neighbors lives on to the next generation.
Any live cell with more than three live neighbors dies, as if by over-population.
Any dead cell with exactly three live neighbors becomes a live cell, as if by reproduction.

The next state of the board is determined by applying the above rules simultaneously to every cell in the current state of the m x n grid board. In this process, births and deaths occur simultaneously.

Given the current state of the board, update the board to reflect its next state.

Note that you do not need to return anything.

Example 1:

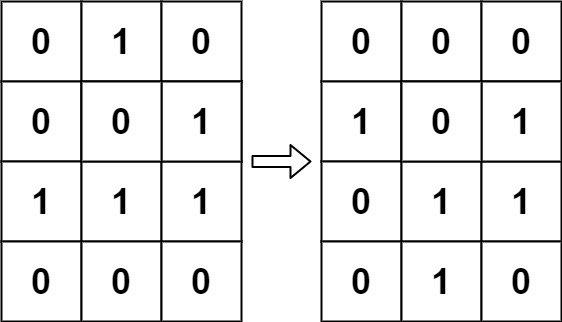
Input: board = [[0,1,0],[0,0,1],[1,1,1],[0,0,0]]
Output: [[0,0,0],[1,0,1],[0,1,1],[0,1,0]]

Example 2:

Input: board = [[1,1],[1,0]]
Output: [[1,1],[1,1]]

Constraints:

m == board.length
n == board[i].length
1 <= m, n <= 25
board[i][j] is 0 or 1.

Follow up:

Could you solve it in-place? Remember that the board needs to be updated simultaneously: You cannot update some cells first and then use their updated values to update other cells.
In this question, we represent the board using a 2D array. In principle, the board is infinite, which would cause problems when the active area encroaches upon the border of the array (i.e., live cells reach the border). How would you address these problems?

Solution

Clarifying Questions

When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:

What are the dimensions constraints for the board (number of rows and columns)?
What are the possible values within the board? Is it strictly binary (0 or 1), or could there be other values?
How should I handle a null or empty board input?
Can I modify the input board directly, or should I create a copy (even though the problem states to do it in place, confirm assumptions)?
Regarding neighbors, do cells on the edge of the board consider cells wrapping around to the opposite edge as neighbors, or are the edges considered boundaries?

Brute Force Solution

Approach

We need to figure out how cells in a grid change from alive to dead or dead to alive based on their neighbors. The brute force way is to look at each cell individually and directly apply the rules based on all its neighbors in the current state.

Here's how the algorithm would work step-by-step:

For every cell in the grid, we're going to figure out what it will be in the next round.
To do this, for each cell, count how many of its neighbors are currently alive.
Once we know the number of alive neighbors, we can directly apply the Game of Life rules.
If the cell is alive and has too few or too many alive neighbors, it will be dead in the next round.
If the cell is dead and has exactly the right number of alive neighbors, it will be alive in the next round.
We repeat this process for every single cell in the entire grid.
Finally, we update the grid all at once to reflect the changes we've calculated for each cell to represent the next round of the game.

Code Implementation

def game_of_life_brute_force(board):
    rows = len(board)
    cols = len(board[0])

    # Create a copy to store the next state
    next_generation_board = [([0] * cols) for _ in range(rows)]

    for row in range(rows):
        for col in range(cols):
            # Count live neighbors for each cell
            live_neighbors_count = count_live_neighbors(board, row, col)

            # Apply game rules to determine next state
            if board[row][col] == 1:
                # Cell is alive
                if live_neighbors_count < 2 or live_neighbors_count > 3:
                    next_generation_board[row][col] = 0
                else:
                    next_generation_board[row][col] = 1

            else:
                # Cell is dead
                if live_neighbors_count == 3:
                    # Reproduction: dead cell becomes alive
                    next_generation_board[row][col] = 1
                else:
                    next_generation_board[row][col] = 0

    # Update the original board
    for row in range(rows):
        for col in range(cols):
            board[row][col] = next_generation_board[row][col]

def count_live_neighbors(board, cell_row, cell_col):
    rows = len(board)
    cols = len(board[0])
    live_neighbors = 0

    for i in range(max(0, cell_row - 1), min(rows, cell_row + 2)):
        for j in range(max(0, cell_col - 1), min(cols, cell_col + 2)):
            if (i, j) != (cell_row, cell_col):
                live_neighbors += board[i][j]

    return live_neighbors

Try it yourself on LeetCode

Big(O) Analysis

Time Complexity

O(m*n) – The algorithm iterates through each cell in the grid. The grid has dimensions m x n, where m is the number of rows and n is the number of columns. For each cell, it counts the number of alive neighbors, which takes constant time. Therefore, the dominant operation is visiting each cell in the grid once. This results in a time complexity of O(m*n), where m and n represent the dimensions of the board.

Space Complexity

O(M * N) – The brute force solution described uses a new grid of the same dimensions as the input to store the next state. This temporary grid is used to store the updated values before applying them to the original grid. Therefore, the space complexity is proportional to the number of cells in the grid, which is equal to M multiplied by N where M is the number of rows and N is the number of columns.

Optimal Solution

Approach

The Game of Life involves updating a grid of cells based on their neighbors. The optimal approach avoids modifying the original grid directly during the update, ensuring that each cell's new state is determined by its neighbors' *original* states. This prevents the changes from one cell from affecting the update of its neighbors in the same generation.

Here's how the algorithm would work step-by-step:

Create a copy of the game board to store the next generation's states.
Go through each cell in the original game board.
For each cell, count how many live neighbors it has.
Based on the number of live neighbors and the cell's current state (live or dead), determine the cell's state in the *next* generation according to the Game of Life rules.
Record the *next* generation state in the copied game board, but do not change the original game board yet.
After checking all cells, replace the original game board with the copied game board, effectively updating the game to the next generation.
Repeat this process for each generation to evolve the game.

Code Implementation

def game_of_life(board, number_of_generations):
    rows = len(board)
    cols = len(board[0])

    for _ in range(number_of_generations):
        # Create a copy to store the next generation.
        next_generation_board = [
            [0] * cols for _ in range(rows)
        ]

        for row in range(rows):
            for col in range(cols):
                live_neighbors = 0
                for i in range(max(0, row - 1), min(rows, row + 2)):
                    for j in range(max(0, col - 1), min(cols, col + 2)):
                        if (i, j) != (row, col):
                            live_neighbors += board[i][j]

                # Apply the Game of Life rules.
                if board[row][col] == 1:
                    # Live cell.
                    if live_neighbors < 2 or live_neighbors > 3:
                        next_generation_board[row][col] = 0
                    else:
                        next_generation_board[row][col] = 1
                else:
                    # Dead cell.
                    if live_neighbors == 3:
                        next_generation_board[row][col] = 1
                    else:
                        next_generation_board[row][col] = 0
        # Update the original board after processing all cells.
        for row in range(rows):
            for col in range(cols):
                board[row][col] = next_generation_board[row][col]

    return board

Try it yourself on LeetCode

Big(O) Analysis

Time Complexity

O(m*n) – The algorithm iterates through each cell in the game board. The game board has dimensions m rows and n columns, resulting in a total of m*n cells to process. For each cell, it counts the live neighbors. The neighbor counting operation takes a constant amount of time. Thus the dominant operation is iterating through the entire m*n board once, giving a time complexity of O(m*n).

Space Complexity

O(M*N) – The algorithm creates a copy of the original game board to store the next generation's states. If the original game board has dimensions M rows and N columns, the copied board will also have M rows and N columns. This means the auxiliary space used is proportional to the number of cells in the original board, which is M multiplied by N. Therefore, the space complexity is O(M*N).

Edge Cases

Case	How to Handle
Null or empty board	Return immediately without modification, or throw an IllegalArgumentException depending on the requirements.
1x1 board	The single cell will either die or stay alive based on its initial state, and always have zero neighbors.
1xn or nx1 board (single row or column)	Handle neighbor calculations carefully, considering only the cells to the left/right or top/bottom respectively.
Board with all live cells	All cells except those on corners and edges will die in the next generation; handle neighbor counts to update in-place.
Board with all dead cells	Only cells with exactly three live neighbors could become alive in the next generation; otherwise the board remains unchanged.
Large board (potential memory issues)	In-place modification avoids creating a copy of the board to conserve memory; however, very large boards could still exceed memory limits.
Board with oscillating patterns (e.g., blinker)	The algorithm should correctly simulate these patterns and converge to the next state without infinite loops.
Integer overflow in neighbor count	Since the maximum number of neighbors is 8, an integer is sufficient and no overflow will occur.