Collect Coins in a Tree
HardThere exists an undirected and unrooted tree with n nodes indexed from 0 to n - 1. You are given an integer n and a 2D integer array edges of length n - 1, where edges[i] = [ai, bi] indicates that there is an edge between nodes ai and bi in the tree. You are also given an array coins of size n where coins[i] can be either 0 or 1, where 1 indicates the presence of a coin in the vertex i.
Initially, you choose to start at any vertex in the tree. Then, you can perform the following operations any number of times:
- Collect all the coins that are at a distance of at most
2from the current vertex, or - Move to any adjacent vertex in the tree.
Find the minimum number of edges you need to go through to collect all the coins and go back to the initial vertex.
Note that if you pass an edge several times, you need to count it into the answer several times.
Example 1:
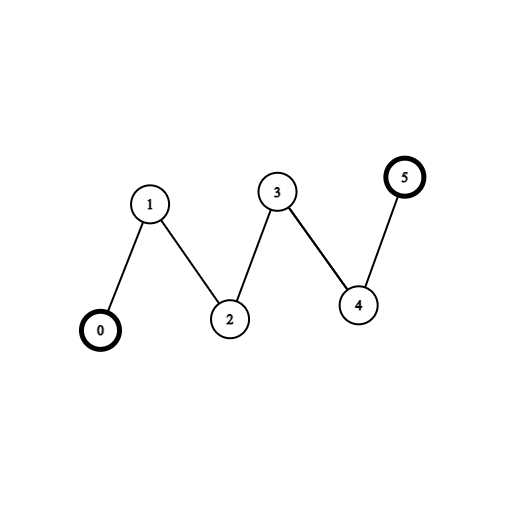
Input: coins = [1,0,0,0,0,1], edges = [[0,1],[1,2],[2,3],[3,4],[4,5]] Output: 2 Explanation: Start at vertex 2, collect the coin at vertex 0, move to vertex 3, collect the coin at vertex 5 then move back to vertex 2.
Example 2:
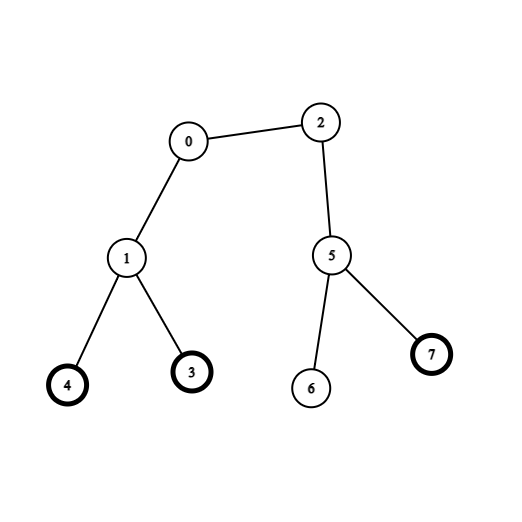
Input: coins = [0,0,0,1,1,0,0,1], edges = [[0,1],[0,2],[1,3],[1,4],[2,5],[5,6],[5,7]] Output: 2 Explanation: Start at vertex 0, collect the coins at vertices 4 and 3, move to vertex 2, collect the coin at vertex 7, then move back to vertex 0.
Constraints:
n == coins.length1 <= n <= 3 * 1040 <= coins[i] <= 1edges.length == n - 1edges[i].length == 20 <= ai, bi < nai != biedgesrepresents a valid tree.
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What are the possible values for the number of nodes 'n' in the tree? Is there a maximum value?
- Are the coin values associated with each node non-negative integers?
- Is the tree represented as an adjacency list or an edge list, and how are the nodes indexed (0-based or 1-based)?
- What should be returned if it's impossible to collect all coins (e.g., if the tree is disconnected and coins exist in multiple components)? Should I return -1, or throw an exception?
- Are there any constraints on the structure of the tree, such as whether it's guaranteed to be a connected graph or whether it might be a forest?
Brute Force Solution
Approach
The brute force method for collecting coins in a tree involves exploring every single possible path you could take. We want to find the best path that lets us collect the most coins while respecting the movement rules within the tree. Basically, we try everything until we discover the optimal solution.
Here's how the algorithm would work step-by-step:
- Start at one specific point (node) in the tree.
- Consider all possible next points (neighboring nodes) you could move to from that point.
- For each of those next points, consider all possible subsequent points, and so on, essentially mapping out every single possible journey through the tree.
- As you explore each journey, keep track of how many coins you've collected.
- Once you've reached the end of a journey (meaning you can't move to any new points), record the total number of coins collected along that specific path.
- Repeat this entire process, starting from every other point in the tree.
- After exploring every possible path from every starting point, compare all the recorded coin totals.
- The path with the highest coin total is the optimal solution.
Code Implementation
def collect_coins_brute_force(edges, coins_on_nodes):
number_of_nodes = len(coins_on_nodes)
maximum_coins_collected = 0
# Iterate through all possible starting nodes
for start_node in range(number_of_nodes):
# Explore paths starting from the current node
current_maximum = explore_all_paths(start_node, edges, coins_on_nodes)
maximum_coins_collected = max(maximum_coins_collected, current_maximum)
return maximum_coins_collected
def explore_all_paths(current_node, edges, coins_on_nodes):
maximum_coins = 0
def depth_first_search(node, visited_nodes, current_coins):
nonlocal maximum_coins
visited_nodes.add(node)
current_coins += coins_on_nodes[node]
maximum_coins = max(maximum_coins, current_coins)
# Explore all neighbors of the current node
neighbors = get_neighbors(node, edges)
# DFS for each unvisited neighbor
for neighbor in neighbors:
if neighbor not in visited_nodes:
depth_first_search(neighbor, visited_nodes.copy(), current_coins)
# Start the depth-first search
depth_first_search(current_node, set(), 0)
return maximum_coins
def get_neighbors(node, edges):
neighboring_nodes = []
for edge_start, edge_end in edges:
if edge_start == node:
neighboring_nodes.append(edge_end)
elif edge_end == node:
neighboring_nodes.append(edge_start)
return neighboring_nodes
# This represents an example usage of the above code.
def example_usage():
edges = [[0, 1], [0, 2], [1, 3], [1, 4], [2, 5], [2, 6]]
coins_on_nodes = [0, 1, 0, 0, 0, 1, 0]
result = collect_coins_brute_force(edges, coins_on_nodes)
print(f"Maximum coins collected: {result}")
if __name__ == "__main__":
example_usage()Big(O) Analysis
Optimal Solution
Approach
The most efficient way to collect the most coins involves removing parts of the tree that won't help us. We repeatedly cut away useless leaves and branches until we are left with the core of the tree containing all the coins.
Here's how the algorithm would work step-by-step:
- First, look at all the leaves (nodes at the edge) of the tree. If a leaf doesn't have a coin, we can remove it because it doesn't contribute to the total.
- Next, look at nodes that are one step away from the leaves. If such a node has only one connection to the rest of the tree, and it also doesn't have a coin, we can remove it too, since you'd never need to go through it.
- Keep repeating the previous two steps, cutting away non-coin-containing leaves and nodes with only one connection that also don't have coins.
- Once you've trimmed as much as possible, the remaining tree contains all the nodes you need to collect the coins. Now, count how many connections (edges) are left in the tree.
- Each connection represents a step you need to take to travel the tree to collect the coins. The total number of steps is the number of edges in the trimmed tree.
Code Implementation
def collect_coins_in_a_tree(number_of_nodes, edges, has_coin):
adjacency_list = [[] for _ in range(number_of_nodes)]
for node1, node2 in edges:
adjacency_list[node1].append(node2)
adjacency_list[node2].append(node1)
nodes_to_keep = [True] * number_of_nodes
while True:
nodes_to_remove = []
# Identify useless leaves
for node_index in range(number_of_nodes):
if nodes_to_keep[node_index] and len(adjacency_list[node_index]) == 1 and not has_coin[node_index]:
nodes_to_remove.append(node_index)
# Identify useless single-connection nodes
for node_index in range(number_of_nodes):
if nodes_to_keep[node_index] and len(adjacency_list[node_index]) <= 1 and not has_coin[node_index]:
nodes_to_remove.append(node_index)
if not nodes_to_remove:
break
for node_to_remove in nodes_to_remove:
if nodes_to_keep[node_to_remove]:
nodes_to_keep[node_to_remove] = False
# This section updates the adjacency list
# after removing a node.
for neighbor_node in adjacency_list[node_to_remove]:
adjacency_list[neighbor_node].remove(node_to_remove)
adjacency_list[node_to_remove] = []
# Count remaining edges
edge_count = 0
for node_index in range(number_of_nodes):
if nodes_to_keep[node_index]:
edge_count += len(adjacency_list[node_index])
# Each edge is counted twice, so divide by 2.
return edge_count // 2Big(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Null or empty tree (no nodes) | Return 0, as there are no coins to collect in an empty tree. |
| Single node tree with a coin | Return 1, since we can collect the coin at the root. |
| Single node tree without a coin | Return 0, as there is nothing to collect. |
| All nodes have coins | The optimal solution might involve traversing most or all of the tree. |
| No nodes have coins | Return 0, because there are no coins to collect regardless of the tree structure. |
| Tree is a straight line (degenerate tree) | The solution should efficiently traverse the line to collect the coins. |
| Very large tree (potential stack overflow if using recursion) | Prefer iterative Depth-First Search (DFS) or Breadth-First Search (BFS) to avoid recursion depth limits. |
| Tree with disconnected components | The prompt implicitly assumes the tree is connected; clarify this assumption and act accordingly based on clarification. |