Delete Node in a BST
MediumGiven a root node reference of a BST and a key, delete the node with the given key in the BST. Return the root node reference (possibly updated) of the BST.
Basically, the deletion can be divided into two stages:
- Search for a node to remove.
- If the node is found, delete the node.
Example 1:
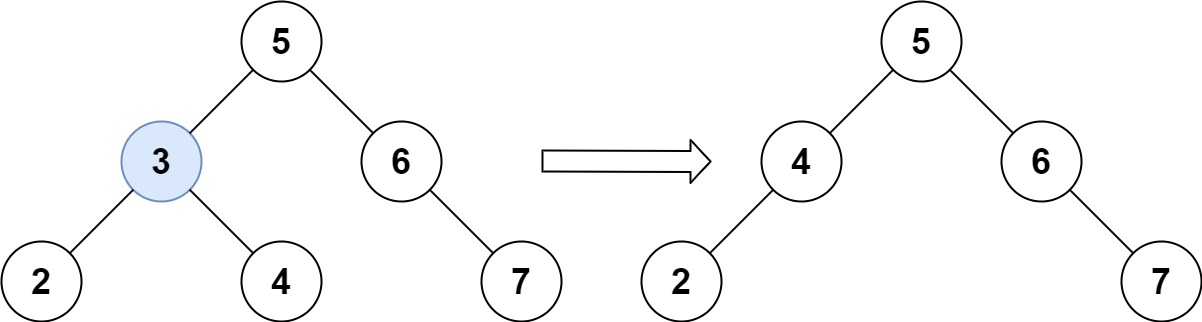
Input: root = [5,3,6,2,4,null,7], key = 3 Output: [5,4,6,2,null,null,7] Explanation: Given key to delete is 3. So we find the node with value 3 and delete it. One valid answer is [5,4,6,2,null,null,7], shown in the above BST. Please notice that another valid answer is [5,2,6,null,4,null,7] and it's also accepted.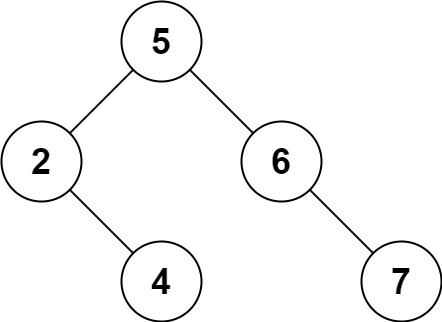
Example 2:
Input: root = [5,3,6,2,4,null,7], key = 0 Output: [5,3,6,2,4,null,7] Explanation: The tree does not contain a node with value = 0.
Example 3:
Input: root = [], key = 0 Output: []
Constraints:
- The number of nodes in the tree is in the range
[0, 104]. -105 <= Node.val <= 105- Each node has a unique value.
rootis a valid binary search tree.-105 <= key <= 105
Follow up: Could you solve it with time complexity O(height of tree)?
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- Can the BST contain duplicate values, and if so, how should they be handled during deletion?
- What should I return if the node to be deleted is not found in the BST? Should I return the original tree, or null?
- Are the values in the BST integers, or can they be other data types like floating-point numbers?
- Is the given BST guaranteed to be valid, or do I need to handle cases where the BST properties are violated?
- Is the 'key' that I need to delete guaranteed to be a value that exists as a node in the tree, or might it be a value that is not present?
Brute Force Solution
Approach
The brute force approach to deleting a node in a Binary Search Tree is like completely rebuilding the tree without the node you want to remove. It involves exploring every possible tree structure after deletion to find a valid one. Think of it as starting from scratch and trying every way to arrange the remaining nodes.
Here's how the algorithm would work step-by-step:
- First, remove the node you want to delete from the tree. This will likely leave a gap or break in the tree structure.
- Imagine you now have all the remaining nodes from the original tree, excluding the deleted one, just sitting in a pile.
- Try every single possible way to arrange these remaining nodes back into a valid Binary Search Tree. This means each node has at most two children, and the nodes are arranged in a way that maintains the BST property (smaller values on the left, larger on the right).
- For each arrangement you create, check if it is a valid Binary Search Tree. A valid BST means that for every node, all nodes in its left subtree are smaller, and all nodes in its right subtree are larger.
- Once you have checked all possible arrangements, choose the one that's a valid Binary Search Tree. This valid BST is the result of deleting the node.
Code Implementation
class Node:
def __init__(self, value):
self.value = value
self.left = None
self.right = None
def delete_node_brute_force(root, key_to_delete):
# Collect all nodes except the one to delete
remaining_nodes = []
def inorder_traversal(node):
if node:
inorder_traversal(node.left)
if node.value != key_to_delete:
remaining_nodes.append(node.value)
inorder_traversal(node.right)
inorder_traversal(root)
if not remaining_nodes:
return None
best_tree = None
# Try all possible arrangements of remaining nodes
import itertools
for permutation in itertools.permutations(remaining_nodes):
new_root = construct_bst(permutation)
if is_valid_bst(new_root):
best_tree = new_root
#Choose the first valid BST
break
return best_tree
def construct_bst(nodes):
if not nodes:
return None
root_value = nodes[0]
root = Node(root_value)
for value in nodes[1:]:
insert_node(root, value)
return root
def insert_node(root, value):
if value < root.value:
if root.left is None:
root.left = Node(value)
else:
insert_node(root.left, value)
else:
if root.right is None:
root.right = Node(value)
else:
insert_node(root.right, value)
def is_valid_bst(root):
#Check if tree satisfies BST property
return is_valid_bst_helper(root, float('-inf'), float('inf'))
def is_valid_bst_helper(node, minimum, maximum):
if not node:
return True
if node.value <= minimum or node.value >= maximum:
return False
#Ensure that left subtree is valid and right subtree is valid
is_left_valid = is_valid_bst_helper(node.left, minimum, node.value)
is_right_valid = is_valid_bst_helper(node.right, node.value, maximum)
return is_left_valid and is_right_validBig(O) Analysis
Optimal Solution
Approach
To remove a node from a Binary Search Tree efficiently, we first locate the node. If found, we need to handle cases based on whether the node has children, strategically replacing it to maintain the BST properties.
Here's how the algorithm would work step-by-step:
- First, we search for the node we want to remove by comparing its value to the values of the nodes we visit as we travel down the tree.
- If we don't find the node, then there's nothing to do, so we're done.
- If the node has no children, we can simply remove it.
- If the node has only one child, we replace the node with its child.
- If the node has two children, we find the smallest node in the right subtree (or the largest in the left subtree).
- We replace the node we want to delete with this smallest (or largest) node's value.
- Finally, we remove the smallest (or largest) node from its original position in the right (or left) subtree, which is easier because it will have at most one child.
Code Implementation
class TreeNode:
def __init__(self, value):
self.value = value
self.left = None
self.right = None
def delete_node_bst(root, key_to_delete):
if not root:
return root
if key_to_delete < root.value:
root.left = delete_node_bst(root.left, key_to_delete)
elif key_to_delete > root.value:
root.right = delete_node_bst(root.right, key_to_delete)
else:
# Node with only one child or no child
if not root.left:
temporary_node = root.right
root = None
return temporary_node
elif not root.right:
temporary_node = root.left
root = None
return temporary_node
# Node with two children:
# Get the inorder successor
# (smallest in the right subtree)
smallest_value_in_right_subtree = find_min_value(root.right)
# Copy the inorder successor's
# content to this node
root.value = smallest_value_in_right_subtree
# Delete the inorder successor
# Because we copied its value up
root.right = delete_node_bst(root.right, smallest_value_in_right_subtree)
return root
def find_min_value(root):
current_node = root
# Find leftmost leaf
while(current_node.left is not None):
current_node = current_node.left
return current_node.valueBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Root is null (empty tree) | Return null immediately as there is nothing to delete in an empty tree. |
| Node to be deleted is the root and has no children | Return null, effectively deleting the entire tree. |
| Node to be deleted is the root and has only a left child | Return the left child as the new root. |
| Node to be deleted is the root and has only a right child | Return the right child as the new root. |
| Node to be deleted has two children; find the inorder successor in the right subtree. | Replace the node to be deleted with its inorder successor and delete the successor from the right subtree. |
| Node to be deleted is not found in the tree. | Return the original root without modification to avoid unintended side effects. |
| Tree contains duplicate keys, and we want to delete one specific instance. | Ensure comparison checks for equality, handles identical values, and deletes the correct node (usually the first found according to the traversal). |
| Deeply unbalanced tree can lead to stack overflow with recursive solutions. | Consider iterative solution if recursion depth is a potential concern. |