Search a 2D Matrix II
MediumWrite an efficient algorithm that searches for a value target in an m x n integer matrix matrix. This matrix has the following properties:
- Integers in each row are sorted in ascending from left to right.
- Integers in each column are sorted in ascending from top to bottom.
Example 1:
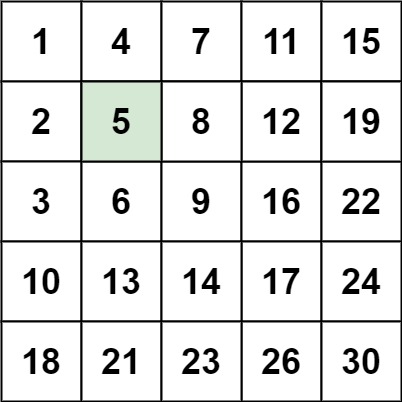
Input: matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5 Output: true
Example 2:
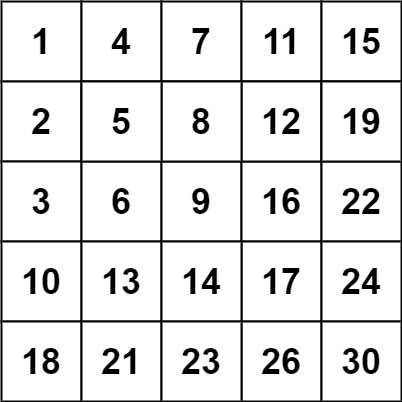
Input: matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20 Output: false
Constraints:
m == matrix.lengthn == matrix[i].length1 <= n, m <= 300-109 <= matrix[i][j] <= 109- All the integers in each row are sorted in ascending order.
- All the integers in each column are sorted in ascending order.
-109 <= target <= 109
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What are the dimensions of the matrix (m and n), and what are the constraints on these values?
- What is the range of integer values within the matrix and for the target value? Could they be negative or zero?
- If the target value appears multiple times in the matrix, should the algorithm return true as soon as it finds the target, or does it need to check the entire matrix?
- What should I return if the input matrix is null or empty?
- Is there a guarantee that the matrix is rectangular (i.e., all rows have the same number of columns)?
Brute Force Solution
Approach
The brute force approach to finding a number in a grid involves checking every single cell. We look at each spot until we either find the number we're looking for or run out of places to check.
Here's how the algorithm would work step-by-step:
- Start at the very first cell in the grid.
- Check if the number in that cell is the number you're searching for.
- If it is, you've found it! Stop searching.
- If it's not, move to the next cell in the grid, going row by row.
- Keep checking each cell one by one.
- If you reach the end of the grid without finding the number, then it's not in the grid.
Code Implementation
def search_matrix_brute_force(matrix, target):
number_of_rows = len(matrix)
number_of_columns = len(matrix[0]) if number_of_rows > 0 else 0
# Iterate through each row of the matrix
for row_index in range(number_of_rows):
# Iterate through each column of the current row
for column_index in range(number_of_columns):
# Check if the current element matches the target
if matrix[row_index][column_index] == target:
return True
# If the target is not found after searching the entire matrix
# return false
return FalseBig(O) Analysis
Optimal Solution
Approach
The key to efficiently searching this special matrix is to start in a corner and eliminate entire rows or columns with each comparison. By moving either left or down depending on the value at the current position, we can quickly narrow down the search area.
Here's how the algorithm would work step-by-step:
- Begin your search at the top-right corner of the matrix.
- Compare the target value with the value at your current position.
- If the target value is smaller, it means the entire column below your current position cannot contain the target, so move one position to the left.
- If the target value is larger, it means the entire row to the left of your current position cannot contain the target, so move one position down.
- Repeat steps 2-4 until you find the target value or move outside the boundaries of the matrix.
- If you move outside the boundaries of the matrix without finding the target, it means the target is not present in the matrix.
Code Implementation
def search_matrix(matrix, target):
if not matrix or not matrix[0]:
return False
number_of_rows = len(matrix)
number_of_columns = len(matrix[0])
row_index = 0
column_index = number_of_columns - 1
while row_index < number_of_rows and column_index >= 0:
current_value = matrix[row_index][column_index]
if current_value == target:
return True
elif target < current_value:
# Target is smaller, eliminate the current column.
column_index -= 1
else:
# Target is larger, eliminate the current row.
row_index += 1
return FalseBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Null or empty matrix | Return false immediately if the matrix is null or has zero rows/columns. |
| Matrix with only one row or one column | The algorithm should work correctly even with a single row or column, effectively becoming a linear search in that row or column. |
| Target is smaller than the smallest element in the matrix | The algorithm should efficiently terminate when the target is smaller than the element at matrix[0][0]. |
| Target is larger than the largest element in the matrix | The algorithm should efficiently terminate when it reaches a boundary where the current element is larger than the target, indicating that the target is not present. |
| Matrix with duplicate values in rows or columns | The algorithm should correctly handle duplicate values without getting stuck or producing incorrect results. |
| Matrix with negative numbers | The algorithm should handle negative numbers correctly, as the sorted nature of rows and columns still holds. |
| Integer overflow when comparing extremely large target values or matrix elements | Consider using long or appropriate data types when comparing target and matrix elements to avoid potential integer overflow. |
| Maximum matrix size causing memory issues | The algorithm should be memory efficient and not consume excessive memory when dealing with very large matrices; binary search approaches are preferrable to approaches requiring extra storage. |