Minimum Area Rectangle II
Medium
0 views
Topics:
ArraysGeometry
You are given an array of points in the X-Y plane points where points[i] = [xi, yi].
Return the minimum area of any rectangle formed from these points, with sides not necessarily parallel to the X and Y axes. If there is not any such rectangle, return 0.
Answers within 10-5 of the actual answer will be accepted.
Example 1:
Input: points = [[1,2],[2,1],[1,0],[0,1]] Output: 2.00000 Explanation: The minimum area rectangle occurs at [1,2],[2,1],[1,0],[0,1], with an area of 2.
Example 2:
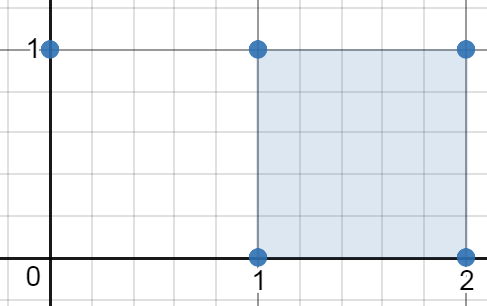
Input: points = [[0,1],[2,1],[1,1],[1,0],[2,0]] Output: 1.00000 Explanation: The minimum area rectangle occurs at [1,0],[1,1],[2,1],[2,0], with an area of 1.
Example 3:
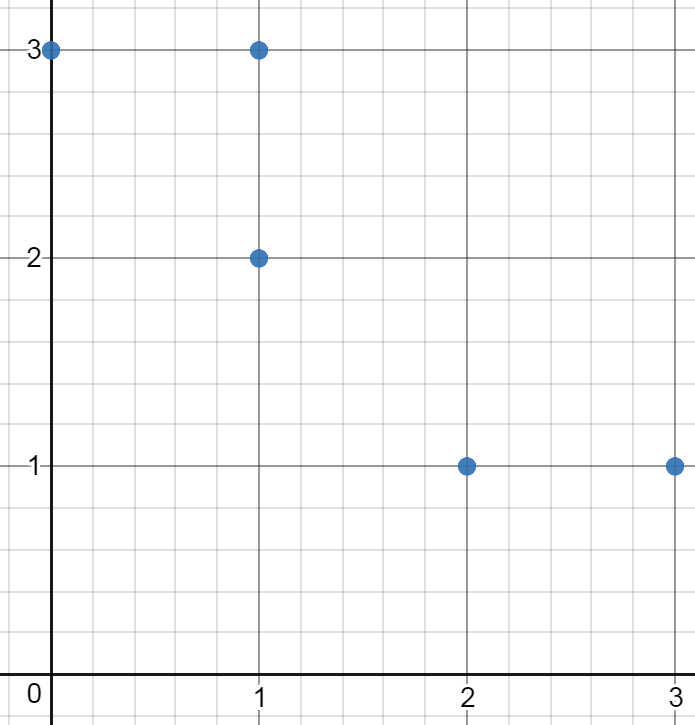
Input: points = [[0,3],[1,2],[3,1],[1,3],[2,1]] Output: 0 Explanation: There is no possible rectangle to form from these points.
Constraints:
1 <= points.length <= 50points[i].length == 20 <= xi, yi <= 4 * 104- All the given points are unique.
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What is the data type of the coordinates? Are they integers or floating-point numbers, and what is the range of possible values?
- If no rectangle can be formed from the given points, what should I return? Should I return null, -1, or some other specific value?
- Are there any constraints on the orientation of the rectangle? Does it have to be parallel to the axes, or can it be rotated?
- Can the input contain duplicate points? If so, how should I handle them?
- If multiple rectangles with the minimum area exist, is it acceptable to return any one of them?
Brute Force Solution
Approach
To find the smallest rectangle, we'll consider every possible combination of four points. We'll check if each combination forms a rectangle and, if so, calculate its area. We keep track of the smallest area found so far, updating it whenever we find a smaller rectangular area.
Here's how the algorithm would work step-by-step:
- Pick any four points from the given set of points.
- Check if the four points form a rectangle.
- To check if it's a rectangle, see if the sides are perpendicular and opposite sides have equal lengths.
- If the four points do form a rectangle, calculate its area.
- Compare the area of this rectangle with the smallest area found so far.
- If the area of the current rectangle is smaller than the smallest area, update the smallest area.
- Repeat the process for every possible combination of four points.
- After checking all combinations, the smallest area we have recorded is the answer.
Code Implementation
import math
def minimum_area_rectangle_ii(points):
number_of_points = len(points)
minimum_rectangle_area = float('inf')
for first_point_index in range(number_of_points):
for second_point_index in range(first_point_index + 1, number_of_points):
for third_point_index in range(second_point_index + 1, number_of_points):
for fourth_point_index in range(third_point_index + 1, number_of_points):
point_one = points[first_point_index]
point_two = points[second_point_index]
point_three = points[third_point_index]
point_four = points[fourth_point_index]
if is_rectangle(point_one, point_two, point_three, point_four):
rectangle_area = calculate_area(point_one, point_two, point_three, point_four)
# Track the minimum area
minimum_rectangle_area = min(minimum_rectangle_area, rectangle_area)
if minimum_rectangle_area == float('inf'):
return 0
else:
return minimum_rectangle_area
def is_rectangle(point_one, point_two, point_three, point_four):
if not is_quadrilateral(point_one, point_two, point_three, point_four):
return False
# Check for perpendicularity
if not (are_perpendicular(point_one, point_two, point_three) or \
are_perpendicular(point_one, point_four, point_three)):
return False
sides = [
distance(point_one, point_two),
distance(point_two, point_three),
distance(point_three, point_four),
distance(point_four, point_one)
]
sides.sort()
# Check that opposite sides have equal length
if not math.isclose(sides[0], sides[1]) or not math.isclose(sides[2], sides[3]):
return False
return True
def is_quadrilateral(point_one, point_two, point_three, point_four):
# Check if any three points are collinear, which would mean it is not a quadrilateral.
if are_collinear(point_one, point_two, point_three) or \
are_collinear(point_one, point_two, point_four) or \
are_collinear(point_one, point_three, point_four) or \
are_collinear(point_two, point_three, point_four):
return False
return True
def are_collinear(point_one, point_two, point_three):
# Formula for area of triangle. If area is 0, points are collinear
return abs(
(point_two[0] - point_one[0]) * (point_three[1] - point_one[1]) - \
(point_three[0] - point_one[0]) * (point_two[1] - point_one[1])
) < 1e-6
def are_perpendicular(point_one, point_two, point_three):
slope_one = slope(point_one, point_two)
slope_two = slope(point_two, point_three)
# Check if slopes are negative reciprocal, meaning they are perpendicular
if slope_one is None or slope_two is None:
return slope_one is not None or slope_two is not None
return math.isclose(slope_one * slope_two, -1)
def slope(point_one, point_two):
# Calculate the slope between two points
if point_one[0] == point_two[0]:
return None
return (point_two[1] - point_one[1]) / (point_two[0] - point_one[0])
def distance(point_one, point_two):
# Standard formula to calculate distance between two points.
return math.sqrt((point_one[0] - point_two[0])**2 + (point_one[1] - point_two[1])**2)
def calculate_area(point_one, point_two, point_three, point_four):
# Assuming it is a rectangle, find lengths of adjacent sides
side_one = distance(point_one, point_two)
side_two = distance(point_two, point_three)
return side_one * side_two
Big(O) Analysis
Time Complexity
O(n^4) – The algorithm considers all possible combinations of four points from the input set of n points. Selecting four points from n can be represented as n choose 4, which is n! / (4! * (n-4)!). This simplifies to an expression proportional to n * (n-1) * (n-2) * (n-3). The process of checking if these four points form a rectangle involves constant time operations for side length and perpendicularity checks. Thus the overall time complexity is dominated by the number of combinations, resulting in O(n^4).
Space Complexity
O(1) – The algorithm iterates through all possible combinations of four points from the input. It involves checking geometric properties and calculating areas, but it does not create any auxiliary data structures that scale with the input size (N, the number of points). Only a few variables are used to store indices, areas, and intermediate calculations, which take up a constant amount of extra space. Therefore, the space complexity is constant.
Optimal Solution
Approach
The challenge is to find the smallest rectangle formed by a given set of points. Instead of checking every possible rectangle, we focus on pairs of points that could be a side of the rectangle, and efficiently search for potential matching sides.
Here's how the algorithm would work step-by-step:
- Consider every pair of points; each pair could be one side of a potential rectangle.
- For each pair (potential side), calculate its length and angle.
- Look for another pair of points that has roughly the same length and angle. If found, these could be parallel sides of a rectangle.
- If we find two pairs that could be parallel sides, we now need to check if we can find the remaining two sides to form a rectangle.
- Calculate the distance from the first side to the second. This distance will be the length of the other two sides if they exist.
- Search for two more points where one is about the calculated distance and perpendicular angle from the first pair of points, and the other is about the calculated distance and perpendicular angle from the second pair of points.
- If all four points are found satisfying the distance and angle constraints, we have a potential rectangle. Calculate the area of this rectangle.
- Keep track of the minimum area found so far, updating it whenever a smaller rectangle is found.
- After checking all possible pairs of points, return the minimum area found.
Code Implementation
import math
def minimum_area_rectangle(points):
number_of_points = len(points)
minimum_area = float('inf')
for i in range(number_of_points):
for j in range(i + 1, number_of_points):
# Consider each pair as a potential side.
point_one_x, point_one_y = points[i]
point_two_x, point_two_y = points[j]
side_length = math.sqrt((point_two_x - point_one_x)**2 + (point_two_y - point_one_y)**2)
side_angle = math.atan2(point_two_y - point_one_y, point_two_x - point_one_x)
for k in range(j + 1, number_of_points):
for l in range(k + 1, number_of_points):
point_three_x, point_three_y = points[k]
point_four_x, point_four_y = points[l]
other_side_length = math.sqrt((point_four_x - point_three_x)**2 + (point_four_y - point_three_y)**2)
other_side_angle = math.atan2(point_four_y - point_three_y, point_four_x - point_three_x)
#Checking parallel sides
if abs(side_length - other_side_length) < 1e-6 and abs(side_angle - other_side_angle) < 1e-6:
distance_between_sides = abs((point_three_x - point_one_x) * math.cos(side_angle) + (point_three_y - point_one_y) * math.sin(side_angle))
# Now, find the other two points
found_point_five = False
found_point_six = False
point_five = None
point_six = None
for m in range(number_of_points):
if m != i and m != j and m != k and m != l:
point_x, point_y = points[m]
#Check for remaining points
perpendicular_angle = side_angle + math.pi / 2
expected_x1 = point_one_x + distance_between_sides * math.cos(perpendicular_angle)
expected_y1 = point_one_y + distance_between_sides * math.sin(perpendicular_angle)
expected_x2 = point_two_x + distance_between_sides * math.cos(perpendicular_angle)
expected_y2 = point_two_y + distance_between_sides * math.sin(perpendicular_angle)
if math.sqrt((point_x - expected_x1)**2 + (point_y - expected_y1)**2) < 1e-6:
found_point_five = True
point_five = (point_x, point_y)
if math.sqrt((point_x - expected_x2)**2 + (point_y - expected_y2)**2) < 1e-6:
found_point_six = True
point_six = (point_x, point_y)
if found_point_five and found_point_six:
area = side_length * distance_between_sides
minimum_area = min(minimum_area, area)
if minimum_area == float('inf'):
return 0.0
else:
return minimum_areaBig(O) Analysis
Time Complexity
O(n^4) – The algorithm iterates through all pairs of points, which contributes O(n^2) to the complexity. For each pair, it searches for another parallel pair, adding another O(n^2) factor. After finding the parallel pairs, checking for the remaining two points that would form a rectangle involves calculations based on distance and angle, but the core search operations are still driven by the initial point pair selections. Therefore, the dominant factor remains O(n^2) nested inside another O(n^2), resulting in O(n^4) time complexity as all possible pairs must be checked.
Space Complexity
O(1) – The algorithm iterates through pairs of points and calculates lengths, angles, and distances. It keeps track of the minimum area found so far. These calculations and the minimum area are stored in a fixed number of variables. Thus, the space used is independent of the number of points (N) and remains constant, resulting in O(1) auxiliary space.
Edge Cases
| Case | How to Handle |
|---|---|
| Empty point list | Return 0 immediately since no rectangle can be formed. |
| Point list with fewer than 4 points | Return 0 immediately since at least 4 points are required to form a rectangle. |
| All points are collinear | Return 0 since no rectangle can be formed with collinear points. |
| Duplicate points in the input list | Ensure that duplicate points don't lead to zero area or invalid rectangle detections; the algorithm should treat them as distinct for calculations. |
| Integer overflow during area calculations | Use appropriate data types (e.g., long) to store area values to prevent overflow. |
| Floating-point precision errors when comparing slopes or distances | Use a small epsilon value for comparing floating-point numbers to account for precision errors. |
| Very large number of points causing performance issues | Optimize the algorithm to minimize the number of slope/distance comparisons. |
| Points forming a square | Ensure that the algorithm correctly identifies squares, as they are a special case of rectangles. |
Explore Interview QuestionsGoogle Interview QuestionsMeta Interview QuestionsAmazon Interview QuestionsApple Interview QuestionsNetflix Interview Questions
Explore Jobs By LevelEntry-Level Software Engineer JobsMid-Level Software Engineer JobsSenior Software Engineer JobsStaff Software Engineer Jobs
