Balanced Binary Tree
EasyGiven a binary tree, determine if it is height-balanced.
Example 1:
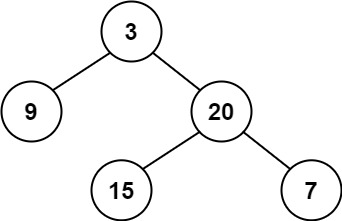
Input: root = [3,9,20,null,null,15,7] Output: true
Example 2:
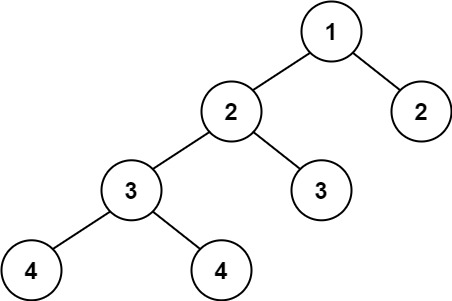
Input: root = [1,2,2,3,3,null,null,4,4] Output: false
Example 3:
Input: root = [] Output: true
Constraints:
- The number of nodes in the tree is in the range
[0, 5000]. -104 <= Node.val <= 104
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- Can the tree be empty (null root)? If so, is an empty tree considered height-balanced?
- Are the node values relevant to determining if the tree is balanced, or only the structure of the tree matters?
- What is the range of possible values for the nodes in the binary tree?
- By 'depth', do you mean the number of nodes along the longest path from the root to a leaf, or the number of edges?
- Is it acceptable to modify the tree structure in any way during the process of determining if it is balanced?
Brute Force Solution
Approach
The brute force approach to check if a tree is balanced is like thoroughly inspecting every single branch. We look at each part of the tree to measure how far it extends down each side.
Here's how the algorithm would work step-by-step:
- Start by looking at the very top of the tree.
- From there, go all the way down the left side and count how many levels deep it goes.
- Then, go all the way down the right side and count how many levels deep it goes.
- Check if the difference between the left and right depths is more than one. If it is, the tree is not balanced.
- If the difference is one or less, then look at the part of the tree on the left. Repeat the process of finding the left and right depths and checking the difference.
- Do the same thing for the part of the tree on the right.
- Continue this process, going deeper and deeper into the tree, checking every single branch to see if the left and right sides are within one level of each other.
- If you find any part of the tree where the left and right depths differ by more than one, then the whole tree is not balanced. Only if every single part of the tree passes this check can you say that the entire tree is balanced.
Code Implementation
class TreeNode:
def __init__(self, value=0, left=None, right=None):
self.value = value
self.left = left
self.right = right
def is_balanced_brute_force(root):
if not root:
return True
left_height = get_height(root.left)
right_height = get_height(root.right)
# If height difference is > 1, tree unbalanced.
if abs(left_height - right_height) > 1:
return False
# Recursively check if left and right subtrees are balanced.
return is_balanced_brute_force(root.left) and \
is_balanced_brute_force(root.right)
def get_height(node):
if not node:
return 0
left_subtree_height = get_height(node.left)
right_subtree_height = get_height(node.right)
# Add 1 to account for the current node itself.
return max(left_subtree_height, right_subtree_height) + 1Big(O) Analysis
Optimal Solution
Approach
The most efficient way to check if a tree is balanced is to look at each part only once. We can do this by checking the height of each subtree and if it is balanced at the same time, working our way up from the leaves.
Here's how the algorithm would work step-by-step:
- Start at the very bottom of the tree (the leaves).
- For each node, find out how tall its left and right sides are.
- If the heights of the left and right sides differ by more than one, the tree is not balanced; we can stop immediately.
- If the heights are close enough, we can say the subtree rooted at that node *is* balanced, and we can remember its height (which is the larger of the left and right side heights, plus one).
- Move up to the next node (its parent) and repeat the height calculation and balance check, using the height information we already computed for the lower nodes.
- Keep going until we reach the very top (the root of the tree).
- If we reach the top without finding any unbalanced subtrees, then the entire tree is balanced!
Code Implementation
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
def is_balanced_binary_tree(root):
def check_balance(node):
if not node:
return 0, True
left_height, is_left_balanced = check_balance(node.left)
right_height, is_right_balanced = check_balance(node.right)
# If either subtree is unbalanced, the whole tree is unbalanced
if not is_left_balanced or not is_right_balanced:
return 0, False
height_difference = abs(left_height - right_height)
# Height difference greater than 1 means it's not balanced
if height_difference > 1:
return 0, False
current_height = max(left_height, right_height) + 1
return current_height, True
_, is_balanced = check_balance(root)
return is_balancedBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Null root node | A null tree is considered balanced, so return true immediately. |
| Single node tree | A single node tree is balanced, so return true. |
| Perfectly balanced tree | The algorithm should efficiently handle perfectly balanced trees with minimal recursion depth. |
| Completely unbalanced tree (left or right skewed) | The algorithm should correctly identify an unbalanced tree in worst-case scenarios, even if it leads to O(n) recursion depth. |
| Tree with large height differences between subtrees at a deep level | The height check should propagate back up to the root to correctly identify imbalance even at deeper levels. |
| Tree with very large number of nodes (potential stack overflow with recursion) | Consider alternative iterative approach to prevent stack overflow in extremely deep trees. |
| Tree where height calculations result in integer overflow | Ensure the chosen data type (e.g., int) for height calculations is sufficient or use long to avoid overflow. |
| Tree with duplicate values, affecting subtree balancing | The algorithm's correctness is independent of the node values themselves, and it depends only on the height of subtrees. |