Count Nodes With the Highest Score
Medium
0 views
Topics:
TreesArraysRecursion
There is a binary tree rooted at 0 consisting of n nodes. The nodes are labeled from 0 to n - 1. You are given a 0-indexed integer array parents representing the tree, where parents[i] is the parent of node i. Since node 0 is the root, parents[0] == -1.
Each node has a score. To find the score of a node, consider if the node and the edges connected to it were removed. The tree would become one or more non-empty subtrees. The size of a subtree is the number of the nodes in it. The score of the node is the product of the sizes of all those subtrees.
Return the number of nodes that have the highest score.
Example 1:
Input: parents = [-1,2,0,2,0] Output: 3 Explanation: - The score of node 0 is: 3 * 1 = 3 - The score of node 1 is: 4 = 4 - The score of node 2 is: 1 * 1 * 2 = 2 - The score of node 3 is: 4 = 4 - The score of node 4 is: 4 = 4 The highest score is 4, and three nodes (node 1, node 3, and node 4) have the highest score.
Example 2:
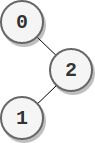
Input: parents = [-1,2,0] Output: 2 Explanation: - The score of node 0 is: 2 = 2 - The score of node 1 is: 2 = 2 - The score of node 2 is: 1 * 1 = 1 The highest score is 2, and two nodes (node 0 and node 1) have the highest score.
Constraints:
n == parents.length2 <= n <= 105parents[0] == -10 <= parents[i] <= n - 1fori != 0parentsrepresents a valid binary tree.
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What is the maximum size of the `parents` array? What is the valid range for the node values (indices in the `parents` array)?
- Can a node have multiple children? If not, what does a value of -1 in the `parents` array signify?
- If multiple nodes have the highest score, should I return the count of these nodes?
- If the input `parents` array is empty or null, what should I return?
- Are the node indices guaranteed to be contiguous and start from 0?
Brute Force Solution
Approach
Imagine a tree where each node has children. We need to calculate a score for each node by multiplying the sizes of the parts of the tree you get if you cut that node off. The brute force method is just figuring out the score for absolutely every node, one at a time.
Here's how the algorithm would work step-by-step:
- Pick the first node in the tree.
- Imagine cutting that node away from the tree. This will split the tree into pieces.
- Count the number of nodes in each of the resulting pieces.
- Multiply those counts together to get the score for that node. If there is only one piece, then the score is simply the count of the node(s). If cutting the node leaves an empty piece, we treat it as having a size of 1.
- Remember this score.
- Now, repeat the process for the second node, the third node, and so on, until you have calculated the score for every single node in the tree.
- Finally, go through all the scores you calculated and count how many nodes have the highest score.
Code Implementation
def count_nodes_with_highest_score(parents):
number_of_nodes = len(parents)
children = [[] for _ in range(number_of_nodes)]
for node_index, parent_index in enumerate(parents):
if parent_index != -1:
children[parent_index].append(node_index)
scores = [0] * number_of_nodes
def calculate_subtree_size(node_index):
subtree_size = 1
for child_index in children[node_index]:
subtree_size += calculate_subtree_size(child_index)
return subtree_size
for node_index in range(number_of_nodes):
product = 1
#Calculate product of sizes of tree parts formed
for child_index in children[node_index]:
product *= calculate_subtree_size(child_index)
remaining_nodes = number_of_nodes - calculate_subtree_size(node_index)
if remaining_nodes > 0:
product *= remaining_nodes
if number_of_nodes == 1:
product = 1
scores[node_index] = product
max_score = 0
count = 0
# Count the nodes with the highest score
for score in scores:
if score > max_score:
max_score = score
count = 1
elif score == max_score:
count += 1
return count
Big(O) Analysis
Time Complexity
O(n²) – We iterate through each of the n nodes in the tree. For each node, we traverse the tree again to compute the sizes of the resulting subtrees after removing the node. This traversal involves visiting each node in the tree, taking O(n) time. Since we repeat this process for each of the n nodes, the overall time complexity is approximately n * n operations. Therefore, the algorithm has a time complexity of O(n²).
Space Complexity
O(N) – The algorithm calculates and remembers a score for each of the N nodes in the tree. This implies storing N scores, requiring an auxiliary array or hash map of size N. In addition, the step of counting nodes in each piece resulting from cutting off a node can be implemented using recursion, potentially leading to a call stack depth of N in the worst-case scenario (e.g., a skewed tree). Therefore, the auxiliary space is determined by the storage of node scores plus the maximum recursion depth, both scaling linearly with N, resulting in a space complexity of O(N).
Optimal Solution
Approach
To efficiently find the nodes with the highest score, we'll traverse the tree structure only once. For each node, we will calculate its score based on its children and parent, and keep track of the highest score seen so far and how many nodes have that score.
Here's how the algorithm would work step-by-step:
- Start by representing the relationships between the nodes in the tree. Think of this as drawing a family tree, but using the given information.
- Now, go through each node in the tree, one by one.
- For each node, figure out its score. This is done by multiplying the sizes of the three groups of nodes that remain if you remove this node from the tree: its left subtree, its right subtree, and the rest of the tree above it.
- Keep track of the highest score you've seen so far as you go through each node.
- Also, keep track of how many nodes have that highest score.
- After checking all the nodes, the number you kept track of tells you how many nodes have the highest possible score.
Code Implementation
def count_highest_score_nodes(parents):
number_of_nodes = len(parents)
children = [[] for _ in range(number_of_nodes)]
for node_index, parent_index in enumerate(parents):
if parent_index != -1:
children[parent_index].append(node_index)
highest_score = 0
highest_score_node_count = 0
def calculate_subtree_size(node_index):
size = 1
for child_index in children[node_index]:
size += calculate_subtree_size(child_index)
subtree_sizes[node_index] = size
return size
subtree_sizes = [0] * number_of_nodes
calculate_subtree_size(0)
for node_index in range(number_of_nodes):
score = 1
# Calculate score based on children sizes
for child_index in children[node_index]:
score *= subtree_sizes[child_index]
# Consider the remaining nodes as well
remaining_nodes = number_of_nodes - subtree_sizes[node_index]
if parents[node_index] != -1:
score *= remaining_nodes
elif number_of_nodes > 1:
score = score
else:
score = 1
# Update the highest score and count
if score > highest_score:
highest_score = score
highest_score_node_count = 1
# Keep track if score matches the highest
elif score == highest_score:
highest_score_node_count += 1
return highest_score_node_countBig(O) Analysis
Time Complexity
O(n) – The algorithm iterates through each of the n nodes in the tree once. For each node, it calculates the score by determining the size of its left subtree, right subtree, and the remaining nodes (its parent's side). Calculating each node's score takes constant time. Updating the highest score and its count also takes constant time per node. Therefore, the total time complexity is proportional to the number of nodes, n, resulting in O(n).
Space Complexity
O(N) – The algorithm implicitly builds a tree structure to represent the relationships between nodes. This tree representation, though not explicitly created as a traditional tree data structure, requires storing child pointers for each node, which consumes O(N) space, where N is the number of nodes. The recursion stack during the tree traversal for calculating subtree sizes can also reach a depth of N in the worst case (skewed tree), contributing O(N) space for the call stack. Therefore, the overall auxiliary space complexity is O(N).
Edge Cases
| Case | How to Handle |
|---|---|
| Null or empty parents array | Return 0 if the input 'parents' array is null or empty, as there are no nodes to process. |
| Single node tree (parents array with only -1) | Return 1, as the single node will always have the highest score. |
| Complete binary tree (or highly balanced tree) leading to potential stack overflow with recursion | Use iterative approach (e.g., using a stack or queue) instead of recursion to avoid potential stack overflow issues. |
| Skewed tree (e.g., linked list structure) | The solution should handle skewed trees efficiently with a linear time complexity. |
| Large number of nodes (close to the maximum constraint) | Ensure the data structures (e.g., arrays, maps) are sized appropriately to avoid memory issues, and use long data type for storing scores. |
| All nodes point to root (parents array contains all -1 except for the root) | The algorithm should correctly compute scores where almost all nodes are directly connected to the root, accounting for disconnected subtrees correctly. |
| Integer overflow when calculating score (product of node counts) | Use long data type to store the node counts and the product to prevent integer overflow during score calculation. |
| Disconnected graph (multiple roots) | The code must handle multiple roots correctly by calculating the score for each and determining the maximum score among them. |
Explore Interview QuestionsGoogle Interview QuestionsMeta Interview QuestionsAmazon Interview QuestionsApple Interview QuestionsNetflix Interview Questions
Explore Jobs By LevelEntry-Level Software Engineer JobsMid-Level Software Engineer JobsSenior Software Engineer JobsStaff Software Engineer Jobs
