Earliest Possible Day of Full Bloom

Hard

Visa

2 views

Topics:

Greedy AlgorithmsArrays

You have n flower seeds. Every seed must be planted first before it can begin to grow, then bloom. Planting a seed takes time and so does the growth of a seed. You are given two 0-indexed integer arrays plantTime and growTime, of length n each:

plantTime[i] is the number of full days it takes you to plant the i^th seed. Every day, you can work on planting exactly one seed. You do not have to work on planting the same seed on consecutive days, but the planting of a seed is not complete until you have worked plantTime[i] days on planting it in total.
growTime[i] is the number of full days it takes the i^th seed to grow after being completely planted. After the last day of its growth, the flower blooms and stays bloomed forever.

From the beginning of day 0, you can plant the seeds in any order.

Return the earliest possible day where all seeds are blooming.

Example 1:

Input: plantTime = [1,4,3], growTime = [2,3,1]
Output: 9
Explanation: The grayed out pots represent planting days, colored pots represent growing days, and the flower represents the day it blooms.
One optimal way is:
On day 0, plant the 0^th seed. The seed grows for 2 full days and blooms on day 3.
On days 1, 2, 3, and 4, plant the 1^st seed. The seed grows for 3 full days and blooms on day 8.
On days 5, 6, and 7, plant the 2^nd seed. The seed grows for 1 full day and blooms on day 9.
Thus, on day 9, all the seeds are blooming.

Example 2:

Input: plantTime = [1,2,3,2], growTime = [2,1,2,1]
Output: 9
Explanation: The grayed out pots represent planting days, colored pots represent growing days, and the flower represents the day it blooms.
One optimal way is:
On day 1, plant the 0^th seed. The seed grows for 2 full days and blooms on day 4.
On days 0 and 3, plant the 1^st seed. The seed grows for 1 full day and blooms on day 5.
On days 2, 4, and 5, plant the 2^nd seed. The seed grows for 2 full days and blooms on day 8.
On days 6 and 7, plant the 3^rd seed. The seed grows for 1 full day and blooms on day 9.
Thus, on day 9, all the seeds are blooming.

Example 3:

Input: plantTime = [1], growTime = [1]
Output: 2
Explanation: On day 0, plant the 0^th seed. The seed grows for 1 full day and blooms on day 2.
Thus, on day 2, all the seeds are blooming.

Constraints:

n == plantTime.length == growTime.length
1 <= n <= 10⁵
1 <= plantTime[i], growTime[i] <= 10⁴

Earliest Possible Day of Full Bloom

Hard

Visa

2 views

Topics:

Greedy AlgorithmsArrays

You have n flower seeds. Every seed must be planted first before it can begin to grow, then bloom. Planting a seed takes time and so does the growth of a seed. You are given two 0-indexed integer arrays plantTime and growTime, of length n each:

plantTime[i] is the number of full days it takes you to plant the i^th seed. Every day, you can work on planting exactly one seed. You do not have to work on planting the same seed on consecutive days, but the planting of a seed is not complete until you have worked plantTime[i] days on planting it in total.
growTime[i] is the number of full days it takes the i^th seed to grow after being completely planted. After the last day of its growth, the flower blooms and stays bloomed forever.

From the beginning of day 0, you can plant the seeds in any order.

Return the earliest possible day where all seeds are blooming.

Example 1:

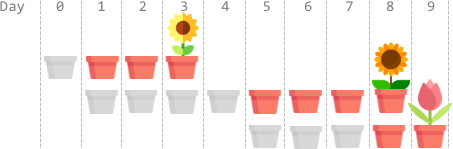
Input: plantTime = [1,4,3], growTime = [2,3,1]
Output: 9
Explanation: The grayed out pots represent planting days, colored pots represent growing days, and the flower represents the day it blooms.
One optimal way is:
On day 0, plant the 0^th seed. The seed grows for 2 full days and blooms on day 3.
On days 1, 2, 3, and 4, plant the 1^st seed. The seed grows for 3 full days and blooms on day 8.
On days 5, 6, and 7, plant the 2^nd seed. The seed grows for 1 full day and blooms on day 9.
Thus, on day 9, all the seeds are blooming.

Example 2:

Input: plantTime = [1,2,3,2], growTime = [2,1,2,1]
Output: 9
Explanation: The grayed out pots represent planting days, colored pots represent growing days, and the flower represents the day it blooms.
One optimal way is:
On day 1, plant the 0^th seed. The seed grows for 2 full days and blooms on day 4.
On days 0 and 3, plant the 1^st seed. The seed grows for 1 full day and blooms on day 5.
On days 2, 4, and 5, plant the 2^nd seed. The seed grows for 2 full days and blooms on day 8.
On days 6 and 7, plant the 3^rd seed. The seed grows for 1 full day and blooms on day 9.
Thus, on day 9, all the seeds are blooming.

Example 3:

Input: plantTime = [1], growTime = [1]
Output: 2
Explanation: On day 0, plant the 0^th seed. The seed grows for 1 full day and blooms on day 2.
Thus, on day 2, all the seeds are blooming.

Constraints:

n == plantTime.length == growTime.length
1 <= n <= 10⁵
1 <= plantTime[i], growTime[i] <= 10⁴

Solution

Clarifying Questions

When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:

What are the possible ranges for the `plantTime` and `growTime` values, and are they always non-negative?
If it's impossible for all flowers to bloom (e.g., due to contradictory plant and grow times), what should the function return?
Do all plants require the same amount of water and sunlight, or can I assume the plant and grow times accurately reflect their individual needs?
If multiple planting orders result in the same earliest bloom day, is any of those orders acceptable?
Is the number of flowers and therefore the lengths of `plantTime` and `growTime` expected to be reasonably small, or are we talking about a potentially very large number of flowers?

Brute Force Solution

Approach

The brute force approach focuses on trying every possible day as the bloom day and checking if all the flowers can bloom by that day, then finding the earliest of such days. It's like trying every single date on the calendar until we find one that works.

Here's how the algorithm would work step-by-step:

Start with the very first day in our possible range of days.
Check if all the flowers have bloomed by that day, considering how long each flower takes to grow and bloom, as well as the time each seed takes to plant.
If they have all bloomed, remember this day as a potential answer.
If not all the flowers have bloomed, move on to the next day and repeat the checking process.
Continue this process until we've checked all possible days.
Once we've tried all days, look at all the days we remembered where all flowers bloomed.
Choose the earliest of those days. That's our answer.

Code Implementation

def earliest_full_bloom_brute_force(plant_time, grow_time):
    number_of_flowers = len(plant_time)
    possible_bloom_days = []
    
    # Iterate through all possible days to find the earliest bloom day
    for current_day in range(1, 100001): 
        all_bloomed = True
        
        # Check if all flowers have bloomed by the current day
        for flower_index in range(number_of_flowers):
            bloom_day = plant_time[flower_index] + grow_time[flower_index]
            if current_day < plant_time[flower_index] + grow_time[flower_index]:
                all_bloomed = False
                break

        # If all flowers have bloomed, store the current day
        if all_bloomed:
            possible_bloom_days.append(current_day)

    # Find the earliest bloom day among all possibilities
    if possible_bloom_days:
        earliest_day = min(possible_bloom_days)
        return earliest_day
    else:
        return -1

Try it yourself on LeetCode

Big(O) Analysis

Time Complexity

O(N*M) – The brute force approach iterates through each possible day, where the number of possible days is proportional to N (the range of bloom days considered). For each day, it checks if all M flowers have bloomed by that day. This check involves iterating through the M flowers and summing their grow times and plant times to compare against the current day. Therefore, the overall time complexity is approximately N*M.

Space Complexity

O(1) – The brute force approach, as described, iterates through possible bloom days and checks if all flowers have bloomed. While trying each day, the algorithm needs to remember if that day resulted in all flowers blooming. It would need to maintain a list of potential bloom days to find the earliest one. However, the provided explanation does not explicitly state the need to store all possible days. It only implies remembering potential bloom days that work. Since the algorithm seeks the earliest day where all flowers bloom, it only needs to remember the earliest bloom day found so far and potentially a boolean flag to indicate if a possible bloom day results in all flowers blooming. Therefore, the auxiliary space remains constant, regardless of the input size N, where N is the number of flowers.

Optimal Solution

Approach

To find the earliest day all flowers bloom, we need to figure out the best planting order. The key is to prioritize planting flowers that take longer to grow earlier in the schedule, so their bloom time doesn't delay the entire process.

Here's how the algorithm would work step-by-step:

Combine the time it takes to plant each flower with how long it takes for it to bloom. Think of these as pairs of numbers.
Reorder these pairs so that the flowers that take the longest to bloom are at the front of the list. This is like sorting by bloom time from longest to shortest.
Start from the beginning of this reordered list. Imagine planting the first flower on day 1.
For each flower, calculate when it will bloom. This is the day you planted it plus how long it takes to bloom. Keep track of the latest bloom day you've seen so far.
When calculating the bloom day for a new flower, make sure you plant it only after you finish planting the previous flower. So, the planting day will be after the previous planting day plus the planting time of the previous flower.
The latest bloom day after you've gone through all the flowers is the earliest possible day they can all be in bloom. This works because you scheduled the most time-consuming bloomers early on.

Code Implementation

def earliest_full_bloom(plant_time, bloom_time):
    number_of_flowers = len(plant_time)
    flower_data = []
    for i in range(number_of_flowers):
        flower_data.append((plant_time[i], bloom_time[i]))

    # Sort flowers by bloom time in descending order
    flower_data.sort(key=lambda x: x[1], reverse=True)

    current_planting_day = 0
    latest_bloom_day = 0

    for planting_time, blooming_time in flower_data:
        # Update current planting day after previous plant
        current_planting_day += planting_time

        #Determine bloom day and update the latest bloom
        bloom_day = current_planting_day + blooming_time
        latest_bloom_day = max(latest_bloom_day, bloom_day)

    return latest_bloom_day

Try it yourself on LeetCode

Big(O) Analysis

Time Complexity

O(n log n) – The dominant operation affecting the time complexity is the sorting of the flower pairs based on their bloom times. Sorting n elements using an efficient algorithm such as merge sort or quicksort takes O(n log n) time. The subsequent loop to calculate bloom days iterates through the n flowers once, taking O(n) time. Since O(n log n) grows faster than O(n), the overall time complexity is determined by the sorting step.

Space Complexity

O(N) – The primary auxiliary space usage comes from creating a list of pairs, where each pair contains the planting time and bloom time for a flower. This list needs to store information for all N flowers, resulting in an auxiliary array of size N. We also store a few variables such as the current planting time and the latest bloom day, which take constant space. Therefore, the overall auxiliary space complexity is dominated by the list of pairs, resulting in O(N) space.

Edge Cases

Case	How to Handle
Empty `plantTime` or `growTime` array	Return 0 if either array is empty, as no plants can be planted.
`plantTime` and `growTime` arrays have different lengths	Throw an IllegalArgumentException since the arrays must have corresponding elements.
All `plantTime` or `growTime` values are 0	The blooming day will be the sum of the plant times (if `growTime` is all 0) or max of grow times (if `plantTime` is all 0), so the algorithm should work correctly.
Large arrays (e.g., length of `plantTime` and `growTime` is 10^5)	Ensure the sorting algorithm used has O(n log n) time complexity to avoid timeouts.
`growTime` values are in descending order	The sorting step based on growTime will reverse this and maximize parallelization benefit, which is intended.
Negative values in `plantTime` or `growTime`	Throw an IllegalArgumentException, as plant and grow times cannot be negative.
Integer overflow when calculating the final bloom day	Use `long` data type to prevent integer overflow when calculating cumulative planting time and bloom day.
`plantTime` and `growTime` have maximum integer values	Using `long` during the calculations should prevent integer overflow, ensuring the answer is correct.