Length of Longest V-Shaped Diagonal Segment

Hard

Visa

1 view

Topics:

Dynamic ProgrammingArrays

You are given a 2D integer matrix grid of size n x m, where each element is either 0, 1, or 2.

A V-shaped diagonal segment is defined as:

The segment starts with 1.
The subsequent elements follow this infinite sequence: 2, 0, 2, 0, ....
The segment:
- Starts along a diagonal direction (top-left to bottom-right, bottom-right to top-left, top-right to bottom-left, or bottom-left to top-right).
- Continues the sequence in the same diagonal direction.
- Makes at most one clockwise 90-degree turn to another diagonal direction while maintaining the sequence.

Return the length of the longest V-shaped diagonal segment. If no valid segment exists, return 0.

Example 1:

Input: grid = [[2,2,1,2,2],[2,0,2,2,0],[2,0,1,1,0],[1,0,2,2,2],[2,0,0,2,2]]

Output: 5

Explanation:

The longest V-shaped diagonal segment has a length of 5 and follows these coordinates: (0,2) → (1,3) → (2,4), takes a 90-degree clockwise turn at (2,4), and continues as (3,3) → (4,2).

Example 2:

Input: grid = [[2,2,2,2,2],[2,0,2,2,0],[2,0,1,1,0],[1,0,2,2,2],[2,0,0,2,2]]

Output: 4

Explanation:

The longest V-shaped diagonal segment has a length of 4 and follows these coordinates: (2,3) → (3,2), takes a 90-degree clockwise turn at (3,2), and continues as (2,1) → (1,0).

Example 3:

Input: grid = [[1,2,2,2,2],[2,2,2,2,0],[2,0,0,0,0],[0,0,2,2,2],[2,0,0,2,0]]

Output: 5

Explanation:

The longest V-shaped diagonal segment has a length of 5 and follows these coordinates: (0,0) → (1,1) → (2,2) → (3,3) → (4,4).

Example 4:

Input: grid = [[1]]

Output: 1

Explanation:

The longest V-shaped diagonal segment has a length of 1 and follows these coordinates: (0,0).

Constraints:

n == grid.length
m == grid[i].length
1 <= n, m <= 500
grid[i][j] is either 0, 1 or 2.

Length of Longest V-Shaped Diagonal Segment

Hard

Visa

1 view

Topics:

Dynamic ProgrammingArrays

You are given a 2D integer matrix grid of size n x m, where each element is either 0, 1, or 2.

A V-shaped diagonal segment is defined as:

The segment starts with 1.
The subsequent elements follow this infinite sequence: 2, 0, 2, 0, ....
The segment:
- Starts along a diagonal direction (top-left to bottom-right, bottom-right to top-left, top-right to bottom-left, or bottom-left to top-right).
- Continues the sequence in the same diagonal direction.
- Makes at most one clockwise 90-degree turn to another diagonal direction while maintaining the sequence.

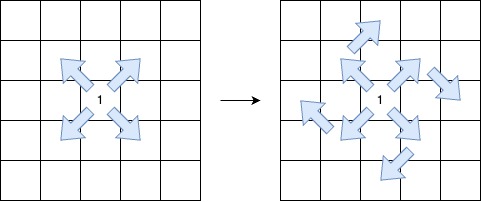
Return the length of the longest V-shaped diagonal segment. If no valid segment exists, return 0.

Example 1:

Input: grid = [[2,2,1,2,2],[2,0,2,2,0],[2,0,1,1,0],[1,0,2,2,2],[2,0,0,2,2]]

Output: 5

Explanation:

The longest V-shaped diagonal segment has a length of 5 and follows these coordinates: (0,2) → (1,3) → (2,4), takes a 90-degree clockwise turn at (2,4), and continues as (3,3) → (4,2).

Example 2:

Input: grid = [[2,2,2,2,2],[2,0,2,2,0],[2,0,1,1,0],[1,0,2,2,2],[2,0,0,2,2]]

Output: 4

Explanation:

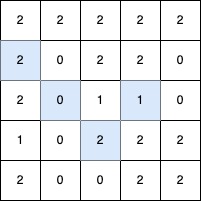
The longest V-shaped diagonal segment has a length of 4 and follows these coordinates: (2,3) → (3,2), takes a 90-degree clockwise turn at (3,2), and continues as (2,1) → (1,0).

Example 3:

Input: grid = [[1,2,2,2,2],[2,2,2,2,0],[2,0,0,0,0],[0,0,2,2,2],[2,0,0,2,0]]

Output: 5

Explanation:

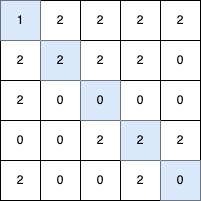
The longest V-shaped diagonal segment has a length of 5 and follows these coordinates: (0,0) → (1,1) → (2,2) → (3,3) → (4,4).

Example 4:

Input: grid = [[1]]

Output: 1

Explanation:

The longest V-shaped diagonal segment has a length of 1 and follows these coordinates: (0,0).

Constraints:

n == grid.length
m == grid[i].length
1 <= n, m <= 500
grid[i][j] is either 0, 1 or 2.

Solution

Clarifying Questions

When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:

What are the possible data types and range of values within the input array?
What should I return if the input array is empty or contains fewer than three elements?
Can the "V" shape be of length zero (i.e., a single element at the bottom)?
If there are multiple longest V-shaped diagonal segments, should I return the length of any one of them, or is there a specific preference (e.g., the one that appears first)?
Could you clarify what you mean by "diagonal segment" in this context? Is the V-shape defined using indices, or values, or both?

Brute Force Solution

Approach

The brute force approach to finding the longest V-shaped diagonal segment involves checking every possible diagonal segment within the given grid. We will check the length of each valid V-shape and select the longest one. We define a valid V-shape as a diagonal path that goes down and then goes up.

Here's how the algorithm would work step-by-step:

Start at every possible position within the grid.
From each starting position, consider all possible lengths for the downward sloping part of the 'V'.
For each downward sloping segment, try all possible lengths for the upward sloping part of the 'V'.
Check if the resulting diagonal path forms a valid 'V' shape, staying within the boundaries of the grid.
Calculate the total length of each valid 'V' shape.
Remember the longest 'V' shape found so far.
Repeat this process for every starting position and combination of downward and upward sloping lengths.
After checking all possible combinations, the remembered longest 'V' shape is the answer.

Code Implementation

def longest_v_shaped_diagonal_segment_brute_force(grid):
    rows = len(grid)
    cols = len(grid[0]) if rows > 0 else 0
    longest_v_length = 0

    for start_row in range(rows):
        for start_col in range(cols):
            # Iterate through all possible start positions.

            for downward_length in range(1, min(rows - start_row, cols - start_col) + 1):
                for upward_length in range(1, min(start_row + downward_length, cols - (start_col - downward_length)) + 1):
                    # Check for valid V shape
                    if start_row + downward_length - upward_length < rows and start_col + downward_length - upward_length < cols and start_row + downward_length - upward_length >= 0 and start_col - downward_length + upward_length >= 0:
                        v_length = downward_length + upward_length - 1

                        # Update if current v-shape is the longest so far
                        longest_v_length = max(longest_v_length, v_length)

    return longest_v_length

Try it yourself on LeetCode

Big(O) Analysis

Time Complexity

O(n^5) – The algorithm iterates through every cell in the grid as a potential starting point, resulting in O(n^2) iterations, where n is the dimension of the grid (assuming a square grid for simplicity). For each starting cell, it explores all possible lengths for the downward sloping segment of the 'V', up to a maximum length of n, leading to O(n) iterations. Then, for each downward segment, it explores all possible lengths for the upward sloping segment, again up to a maximum length of n, adding another O(n) iterations. Checking if each 'V' shape is valid within the grid takes O(n) time in the worst case, as the length of the diagonal could be n. Therefore the total time complexity is O(n^2 * n * n * n) which simplifies to O(n^5).

Space Complexity

O(1) – The brute force approach primarily uses a few variables to store the current starting position, lengths of downward and upward slopes, the current length of the V-shape, and the maximum length found so far. No auxiliary data structures that scale with the input grid's dimensions are used. Therefore, the space complexity remains constant regardless of the input size, implying O(1) space complexity.

Optimal Solution

Approach

The key to efficiently finding the longest 'V' shape is to consider each point in the grid as a potential bottom of the V. We want to extend outwards from each point and track the lengths of the increasing and decreasing parts of the 'V'.

Here's how the algorithm would work step-by-step:

Go through each point in the grid, one at a time.
For each point, imagine it as the lowest point in a 'V' shape.
From that lowest point, look diagonally upwards to the left, counting how many steps you can take where the values are increasing.
From that same lowest point, look diagonally upwards to the right, counting how many steps you can take where the values are increasing.
Add the lengths of the two increasing segments together. This gives you the total length of a potential 'V' shape centered at that point.
Keep track of the longest 'V' shape you find as you check each point. If the current 'V' shape is longer than the previous longest, update the longest.
After checking all points, return the length of the longest 'V' shape you found.

Code Implementation

def find_longest_v_shaped_diagonal_segment(grid):
    if not grid:
        return 0

    number_of_rows = len(grid)
    number_of_columns = len(grid[0])
    longest_v_shape_length = 0

    for row_index in range(number_of_rows):
        for column_index in range(number_of_columns):
            # Consider each point as the bottom of the 'V'
            left_increasing_length = 0
            right_increasing_length = 0

            # Calculate increasing length to the left diagonal
            current_row = row_index - 1
            current_column = column_index - 1

            while current_row >= 0 and current_column >= 0:
                if grid[current_row][current_column] > grid[current_row + 1][current_column + 1]:
                    left_increasing_length += 1
                    current_row -= 1
                    current_column -= 1
                else:
                    break

            # Calculate increasing length to the right diagonal
            current_row = row_index - 1
            current_column = column_index + 1

            while current_row >= 0 and current_column < number_of_columns:
                if grid[current_row][current_column] > grid[current_row + 1][current_column - 1]:
                    right_increasing_length += 1
                    current_row -= 1
                    current_column += 1
                else:
                    break

            # Total length is the sum of the two increasing segments
            total_length = left_increasing_length + right_increasing_length

            # Update max length if current is longer
            longest_v_shape_length = max(longest_v_shape_length, total_length)

    return longest_v_shape_length

Try it yourself on LeetCode

Big(O) Analysis

Time Complexity

O(n*m) – The algorithm iterates through each cell of the grid, which has a size of n rows and m columns, contributing a factor of n*m. For each cell, it extends diagonally upwards to the left and right, with the maximum length of each diagonal being proportional to the minimum of n and m. Therefore, the runtime for each cell is O(min(n, m)). Considering we visit each cell in the grid and for each cell, we do work of O(min(n, m)), the overall time complexity is O(n*m * min(n,m)). In the worst case where n=m, this simplifies to O(n^3), but given the problem description, we'll treat these separately, thus the dominant term becomes O(n*m).

Space Complexity

O(1) – The plain English explanation describes iterating through each point in the grid and calculating the V-shape length centered at that point. It only mentions tracking the longest V-shape length found so far, which can be stored in a single variable. There are no temporary lists, hash maps, or other data structures created or used within the algorithm described. Therefore, the auxiliary space required is constant and independent of the input grid's size.

Edge Cases

Case	How to Handle
Null or empty 2D array	Return 0 since there are no diagonals to traverse.
2D array with only one row or one column	Return 0 as a V-shaped diagonal requires at least two rows and two columns.
2D array where all elements are identical	Return 0 because a V-shape requires increasing/decreasing values, which identical elements lack.
Integer overflow when calculating diagonal sums or lengths	Use a data type that can accommodate large sums (e.g., long) or check for potential overflows before they occur.
Non-square 2D array (different number of rows and columns)	The algorithm should still correctly identify V-shaped diagonals regardless of whether the array is square.
Negative numbers in the 2D array	The algorithm must correctly handle negative numbers when determining increasing/decreasing trends along diagonals.
2D array with very large dimensions (potential memory issues)	Consider a more memory-efficient approach if the array is excessively large; iterative solutions are better for this case.
No V-shaped diagonals exist in the array	The algorithm should return 0 in this case, indicating no valid V-shaped diagonal segments were found.