Diagonal Traverse
MediumGiven an m x n matrix mat, return an array of all the elements of the array in a diagonal order.
Example 1:
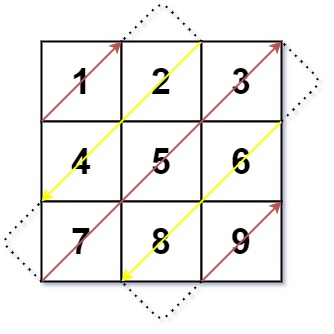
Input: mat = [[1,2,3],[4,5,6],[7,8,9]] Output: [1,2,4,7,5,3,6,8,9]
Example 2:
Input: mat = [[1,2],[3,4]] Output: [1,2,3,4]
Constraints:
m == mat.lengthn == mat[i].length1 <= m, n <= 1041 <= m * n <= 104-105 <= mat[i][j] <= 105
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What are the dimensions of the matrix (number of rows and columns)? Can I assume it's always a rectangular matrix?
- Can the matrix be empty (either 0 rows or 0 columns), or can a row be empty?
- What is the expected output if the input matrix is null or empty?
- What data type are the elements within the matrix? Are negative numbers, zeros, or floating-point numbers possible?
- In the diagonal traversal, if we reach the edge of the matrix, which direction should we prioritize if both a horizontal and vertical move are possible?
Brute Force Solution
Approach
Imagine you're reading a grid of numbers diagonally. The brute force method involves methodically visiting each number in the grid by following the diagonals one by one, going up and down. We essentially trace every diagonal, recording the numbers we encounter.
Here's how the algorithm would work step-by-step:
- Begin at the very first number in the grid.
- Travel diagonally upwards and to the right, recording each number you find until you hit the edge of the grid.
- If you hit the right edge, move down one row. If you hit the top edge, move right one column. Start a new diagonal path.
- Again travel diagonally downwards and to the left, recording each number you find until you hit the edge of the grid.
- If you hit the left edge, move down one row. If you hit the bottom edge, move right one column. Start a new diagonal path.
- Keep switching directions, zig-zagging up and down the diagonals until every number in the grid has been visited and recorded in the order they were encountered.
Code Implementation
def diagonal_traverse_brute_force(matrix):
if not matrix:
return []
number_of_rows = len(matrix)
number_of_columns = len(matrix[0])
result = []
row = 0
column = 0
going_up = True
for _ in range(number_of_rows * number_of_columns):
result.append(matrix[row][column])
if going_up:
new_row = row - 1
new_column = column + 1
if new_row < 0 and new_column < number_of_columns:
# Hit the top edge, move right
row = 0
column = new_column
elif new_column == number_of_columns and new_row >= 0:
# Hit the right edge, move down
column = number_of_columns - 1
row = new_row + 2
elif new_row < 0 and new_column == number_of_columns:
# Hit the top-right corner, move down
row = 1
column = number_of_columns - 1
else:
row = new_row
column = new_column
if new_row < 0 or new_column == number_of_columns:
going_up = False
else:
new_row = row + 1
new_column = column - 1
if new_column < 0 and new_row < number_of_rows:
# Hit the left edge, move down
column = 0
row = new_row
elif new_row == number_of_rows and new_column >= 0:
# Hit the bottom edge, move right
row = number_of_rows - 1
column = new_column + 2
elif new_column < 0 and new_row == number_of_rows:
# Hit the bottom-left corner, move right
row = number_of_rows - 1
column = 1
else:
row = new_row
column = new_column
# Change direction at the edges
if new_row == number_of_rows or new_column < 0:
going_up = True
return resultBig(O) Analysis
Optimal Solution
Approach
The optimal approach involves navigating the matrix diagonally, changing direction at the boundaries. We trace each diagonal in the correct order, collecting the elements as we go, without explicitly checking every single element in the matrix.
Here's how the algorithm would work step-by-step:
- Imagine you are walking along diagonals starting from the top-left of the matrix.
- Move along a diagonal, collecting each number you encounter.
- When you hit a boundary (top or right edge), change your direction downwards and to the left.
- When you hit another boundary (bottom or left edge), change your direction upwards and to the right.
- Continue traversing the matrix in this zigzag fashion until you have collected all numbers.
- The order in which you collect the numbers is the required diagonal traversal order.
Code Implementation
def diagonal_traverse(matrix):
if not matrix or not matrix[0]:
return []
number_of_rows = len(matrix)
number_of_columns = len(matrix[0])
result = []
row = 0
column = 0
up = True
for _ in range(number_of_rows * number_of_columns):
result.append(matrix[row][column])
if up:
new_row = row - 1
new_column = column + 1
# Changing direction because we hit the top boundary
if new_row < 0 and new_column < number_of_columns:
row = 0
column = new_column
up = False
elif new_row < 0 and new_column >= number_of_columns:
row = row + 1
column = number_of_columns - 1
up = False
elif new_column >= number_of_columns:
row = new_row + 2
column = number_of_columns - 1
up = False
else:
row = new_row
column = new_column
else:
new_row = row + 1
new_column = column - 1
# Changing direction because we hit the left boundary.
if new_column < 0 and new_row < number_of_rows:
row = new_row
column = 0
up = True
elif new_column < 0 and new_row >= number_of_rows:
row = number_of_rows - 1
column = new_column + 2
up = True
elif new_row >= number_of_rows:
row = number_of_rows - 1
column = new_column + 2
up = True
else:
row = new_row
column = new_column
return resultBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Null or empty matrix | Return an empty list to handle invalid input gracefully. |
| Matrix with only one row | Iterate through the single row and add elements to the result list. |
| Matrix with only one column | Iterate through the single column and add elements to the result list. |
| Square matrix with a large size (N x N) | Ensure the solution's time and space complexity are efficient enough to handle large inputs; consider the impact of memory allocation. |
| Rectangular matrix with dimensions (1 x N) or (N x 1) | Handle these cases similarly to the single row/column cases above, ensuring correct traversal. |
| Rectangular matrix with dimensions (M x N) where M != N | Adjust the direction change and boundary checks based on the dimensions of the non-square matrix. |
| Matrix containing negative numbers or zeros | The algorithm should work correctly regardless of the number values, as it depends on indices. |
| Integer overflow during index calculations | Use appropriate data types (e.g., long) to prevent integer overflow when calculating row and column indices. |