Binary Tree Postorder Traversal
Given the root of a binary tree, return the postorder traversal of its nodes' values.
Example 1:
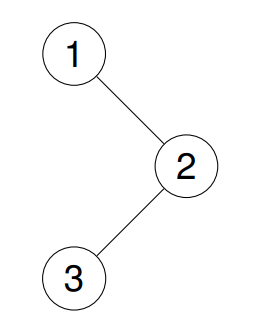
Input: root = [1,null,2,3]
Output: [3,2,1]
Explanation:
Example 2:
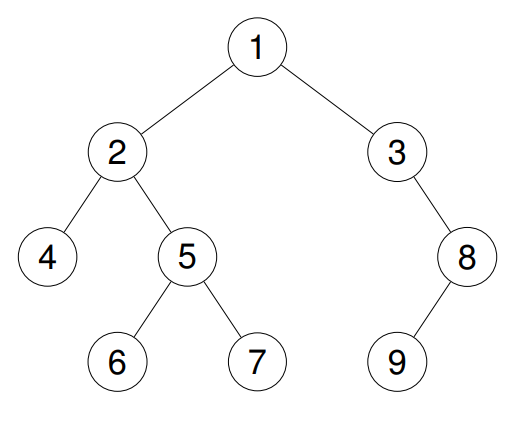
Input: root = [1,2,3,4,5,null,8,null,null,6,7,9]
Output: [4,6,7,5,2,9,8,3,1]
Explanation:
Example 3:
Input: root = []
Output: []
Example 4:
Input: root = [1]
Output: [1]
Constraints:
- The number of the nodes in the tree is in the range
[0, 100]. -100 <= Node.val <= 100
Follow up: Recursive solution is trivial, could you do it iteratively?
#include <iostream>
#include <vector>
#include <stack>
using namespace std;
// Definition for a binary tree node.
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode() : val(0), left(nullptr), right(nullptr) {}
TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};
// Recursive Solution
vector<int> postorderTraversalRecursive(TreeNode* root) {
vector<int> result;
if (root == nullptr) {
return result;
}
vector<int> leftSubtree = postorderTraversalRecursive(root->left);
result.insert(result.end(), leftSubtree.begin(), leftSubtree.end());
vector<int> rightSubtree = postorderTraversalRecursive(root->right);
result.insert(result.end(), rightSubtree.begin(), rightSubtree.end());
result.push_back(root->val);
return result;
}
// Iterative Solution using two stacks
vector<int> postorderTraversalIterative(TreeNode* root) {
vector<int> result;
if (root == nullptr) {
return result;
}
stack<TreeNode*> s1, s2;
s1.push(root);
while (!s1.empty()) {
TreeNode* node = s1.top();
s1.pop();
s2.push(node);
if (node->left) {
s1.push(node->left);
}
if (node->right) {
s1.push(node->right);
}
}
while (!s2.empty()) {
result.push_back(s2.top()->val);
s2.pop();
}
return result;
}
//Iterative Solution using one stack
vector<int> postorderTraversalIterativeSingleStack(TreeNode* root) {
vector<int> result;
if (!root) return result;
stack<TreeNode*> stack;
TreeNode* lastVisited = nullptr;
while (root || !stack.empty()) {
if (root) {
stack.push(root);
root = root->left;
} else {
TreeNode* topNode = stack.top();
// If right child exists and is not visited
if (topNode->right && topNode->right != lastVisited) {
root = topNode->right;
} else {
result.push_back(topNode->val);
lastVisited = topNode;
stack.pop();
}
}
}
return result;
}
int main() {
// Example usage:
TreeNode* root = new TreeNode(1);
root->right = new TreeNode(2);
root->right->left = new TreeNode(3);
cout << "Recursive Postorder Traversal: ";
vector<int> recursiveResult = postorderTraversalRecursive(root);
for (int val : recursiveResult) {
cout << val << " ";
}
cout << endl;
cout << "Iterative Postorder Traversal (Two Stacks): ";
vector<int> iterativeResult = postorderTraversalIterative(root);
for (int val : iterativeResult) {
cout << val << " ";
}
cout << endl;
cout << "Iterative Postorder Traversal (Single Stack): ";
vector<int> iterativeSingleStackResult = postorderTraversalIterativeSingleStack(root);
for (int val : iterativeSingleStackResult) {
cout << val << " ";
}
cout << endl;
// Clean up memory (important!)
delete root->right->left;
delete root->right;
delete root;
return 0;
}
Explanation
Given a binary tree, the goal is to return the postorder traversal of its nodes' values. Postorder traversal means visiting the left subtree, then the right subtree, and finally the root node.
1. Recursive Solution
The recursive approach is straightforward and mirrors the definition of postorder traversal.
Algorithm:
- Base Case: If the root is
nullptr, return an empty vector. - Recursively traverse the left subtree.
- Recursively traverse the right subtree.
- Append the value of the root node to the result.
2. Iterative Solution (Two Stacks)
The iterative solution uses two stacks to simulate the recursive calls.
Algorithm:
- Push the root node onto the first stack (
s1). - While
s1is not empty:- Pop a node from
s1and push it onto the second stack (s2). - Push the left child of the node onto
s1(if it exists). - Push the right child of the node onto
s1(if it exists).
- Pop a node from
- While
s2is not empty, pop nodes froms2and add their values to the result vector. Sinces2contains the nodes in reverse postorder, popping them gives the correct postorder sequence.
3. Iterative Solution (Single Stack)
This iterative solution optimizes space by using only one stack.
Algorithm:
- Initialize an empty stack.
- Keep going left until you hit a null, pushing each node onto the stack.
- From the top of the stack, look at its right child.
- If it has a right child that's NOT already visited, visit that right child from step 2.
- If it has NO right child, or the right child WAS already visited, process the top of the stack (add to
resultand pop off the stack), making note that you've visited it.
Big O Analysis
Recursive Solution
- Time Complexity: O(N), where N is the number of nodes in the tree. Each node is visited once.
- Space Complexity: O(H), where H is the height of the tree, due to the recursive call stack. In the worst case (skewed tree), H = N, so it becomes O(N). In the best case (balanced tree), H = log N, so it becomes O(log N).
Iterative Solution (Two Stacks)
- Time Complexity: O(N), where N is the number of nodes in the tree. Each node is visited and pushed/popped from the stacks.
- Space Complexity: O(N), where N is the number of nodes in the tree. In the worst case, the stacks can contain all nodes of the tree.
Iterative Solution (Single Stack)
- Time Complexity: O(N), where N is the number of nodes in the tree. Each node is visited.
- Space Complexity: O(H), where H is the height of the tree. In the worst case (skewed tree) H = N, in the best case (balanced tree), H = log N.