K Radius Subarray Averages Interview Question for Apple

You are given a 0-indexed array nums of n integers, and an integer k.

The k-radius average for a subarray of nums centered at some index i with the radius k is the average of all elements in nums between the indices i - k and i + k (inclusive). If there are less than k elements before or after the index i, then the k-radius average is -1.

Build and return an array avgs of length n where avgs[i] is the k-radius average for the subarray centered at index i.

The average of x elements is the sum of the x elements divided by x, using integer division. The integer division truncates toward zero, which means losing its fractional part.

For example, the average of four elements 2, 3, 1, and 5 is (2 + 3 + 1 + 5) / 4 = 11 / 4 = 2.75, which truncates to 2.

Example 1:

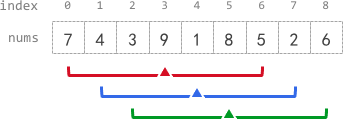
Input: nums = [7,4,3,9,1,8,5,2,6], k = 3
Output: [-1,-1,-1,5,4,4,-1,-1,-1]
Explanation:
- avg[0], avg[1], and avg[2] are -1 because there are less than k elements before each index.
- The sum of the subarray centered at index 3 with radius 3 is: 7 + 4 + 3 + 9 + 1 + 8 + 5 = 37.
  Using integer division, avg[3] = 37 / 7 = 5.
- For the subarray centered at index 4, avg[4] = (4 + 3 + 9 + 1 + 8 + 5 + 2) / 7 = 4.
- For the subarray centered at index 5, avg[5] = (3 + 9 + 1 + 8 + 5 + 2 + 6) / 7 = 4.
- avg[6], avg[7], and avg[8] are -1 because there are less than k elements after each index.

Example 2:

Input: nums = [100000], k = 0
Output: [100000]
Explanation:
- The sum of the subarray centered at index 0 with radius 0 is: 100000.
  avg[0] = 100000 / 1 = 100000.

Example 3:

Input: nums = [8], k = 100000
Output: [-1]
Explanation: 
- avg[0] is -1 because there are less than k elements before and after index 0.

Given an array of integers, `nums`, and an integer `k`, find the k-radius average for each subarray centered at index `i` with radius `k`. The k-radius average is the average of all elements in `nums` between the indices `i - k` and `i + k` (inclusive). If there are less than `k` elements before or after the index `i`, the k-radius average is -1. For example, if `nums = [7,4,3,9,1,8,5,2,6]` and `k = 3`, then the output should be `[-1,-1,-1,5,4,4,-1,-1,-1]`.

class Solution {
    public int[] getAverages(int[] nums, int k) {
        int n = nums.length;
        int[] avgs = new int[n];
        Arrays.fill(avgs, -1);

        if (k > n / 2) {
            return avgs;
        }

        long[] prefixSum = new long[n + 1];
        for (int i = 0; i < n; i++) {
            prefixSum[i + 1] = prefixSum[i] + nums[i];
        }

        for (int i = k; i < n - k; i++) {
            long windowSum = prefixSum[i + k + 1] - prefixSum[i - k];
            avgs[i] = (int) (windowSum / (2 * k + 1));
        }

        return avgs;
    }
}

Naive Solution

The naive solution would involve iterating through each index i in nums and calculating the sum of the subarray centered at i with radius k. For each index, we would iterate from i - k to i + k, summing the elements. If i - k < 0 or i + k >= n, we would set avgs[i] to -1.

// Naive Solution (Time Limit Exceeded for larger inputs)
class Solution {
    public int[] getAverages(int[] nums, int k) {
        int n = nums.length;
        int[] avgs = new int[n];
        Arrays.fill(avgs, -1);

        for (int i = 0; i < n; i++) {
            if (i - k >= 0 && i + k < n) {
                long sum = 0;
                for (int j = i - k; j <= i + k; j++) {
                    sum += nums[j];
                }
                avgs[i] = (int) (sum / (2 * k + 1));
            }
        }

        return avgs;
    }
}

Optimal Solution

The optimal solution uses the prefix sum technique to calculate the sum of each subarray in O(1) time. First, we compute the prefix sum array prefixSum such that prefixSum[i] stores the sum of the first i elements in nums. Then, for each index i, the sum of the subarray centered at i with radius k is prefixSum[i + k + 1] - prefixSum[i - k]. We divide this sum by 2 * k + 1 to get the average.

class Solution {
    public int[] getAverages(int[] nums, int k) {
        int n = nums.length;
        int[] avgs = new int[n];
        Arrays.fill(avgs, -1);

        if (k > n / 2) {
            return avgs;
        }

        long[] prefixSum = new long[n + 1];
        for (int i = 0; i < n; i++) {
            prefixSum[i + 1] = prefixSum[i] + nums[i];
        }

        for (int i = k; i < n - k; i++) {
            long windowSum = prefixSum[i + k + 1] - prefixSum[i - k];
            avgs[i] = (int) (windowSum / (2 * k + 1));
        }

        return avgs;
    }
}

Big(O) Run-time Analysis

Optimal Solution:
- Calculating the prefix sum array takes O(n) time.
- Iterating through the array to calculate the averages takes O(n) time.
- Therefore, the overall run-time complexity is O(n).
Naive Solution:
- Iterating through each element of the array O(n)
- Calculating the sum of elements from i - k to i + k takes O(2k) which simplifies to O(k)
- Therefore, the overall run-time complexity is O(n * k)

Big(O) Space Usage Analysis

Optimal Solution:
- The prefix sum array takes O(n) space.
- The avgs array takes O(n) space.
- Therefore, the overall space complexity is O(n).
Naive Solution:
- The avgs array takes O(n) space.
- Therefore, the overall space complexity is O(n).

Edge Cases

k = 0: The radius is 0, so the average at each index i is just nums[i]. This case is handled correctly by the provided solution.
k > n / 2: If k is larger than half the array size, then no index will have k elements before and after it. In this case, the problem specifies that every element of the result array should be -1. The code provided handles this case as the very first check.
Large Input Values: The sum of the elements in the window i - k to i + k could potentially exceed the maximum value of an int. Using long for prefixSum and windowSum prevents overflow.
n = 1: If the input array has only one element. If k = 0, we would return that element. If k > 0, we would return -1, which is correctly handled.