Binary Tree Coloring Game Interview Question for Google

Two players play a turn based game on a binary tree. We are given the root of this binary tree, and the number of nodes n in the tree. n is odd, and each node has a distinct value from 1 to n.

Initially, the first player names a value x with 1 <= x <= n, and the second player names a value y with 1 <= y <= n and y != x. The first player colors the node with value x red, and the second player colors the node with value y blue.

Then, the players take turns starting with the first player. In each turn, that player chooses a node of their color (red if player 1, blue if player 2) and colors an uncolored neighbor of the chosen node (either the left child, right child, or parent of the chosen node.)

If (and only if) a player cannot choose such a node in this way, they must pass their turn. If both players pass their turn, the game ends, and the winner is the player that colored more nodes.

You are the second player. If it is possible to choose such a y to ensure you win the game, return true. If it is not possible, return false.

Example 1:

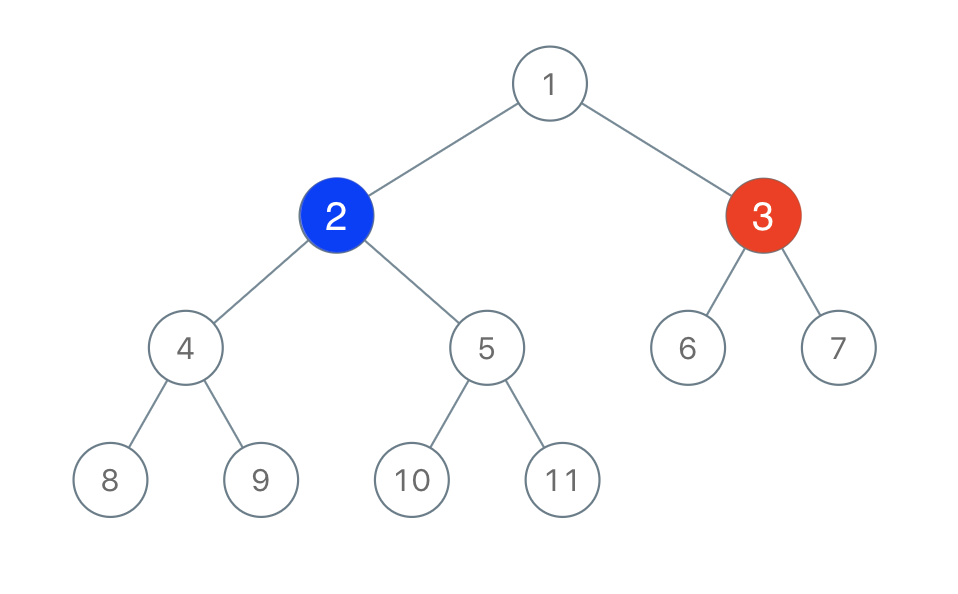
Input: root = [1,2,3,4,5,6,7,8,9,10,11], n = 11, x = 3
Output: true
Explanation: The second player can choose the node with value 2.

Example 2:

Input: root = [1,2,3], n = 3, x = 1
Output: false

Constraints:

The number of nodes in the tree is n.
1 <= x <= n <= 100
n is odd.
1 <= Node.val <= n
All the values of the tree are unique.

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def btreeGameWinningMove(self, root: Optional[TreeNode], n: int, x: int) -> bool:
        self.left_count = 0
        self.right_count = 0
        
        def count_nodes(node, x):
            if not node:
                return 0
            
            left = count_nodes(node.left, x)
            right = count_nodes(node.right, x)
            
            if node.val == x:
                self.left_count = left
                self.right_count = right
                
            return left + right + 1
            
        count_nodes(root, x)
        
        parent_count = n - (self.left_count + self.right_count + 1)
        
        return max(parent_count, self.left_count, self.right_count) > n // 2

Naive Solution

A naive approach would involve simulating the game for all possible choices of y and determining if the second player wins. This would be highly inefficient, especially for larger trees.

Optimal Solution

The key insight is that the second player can win if they choose a node y such that the subtree rooted at y or the remaining part of the tree (excluding the subtree rooted at x) has more than n // 2 nodes. The node x splits the tree into three parts: the left subtree of x, the right subtree of x, and the remaining tree (the parent part). The second player should choose y such that they can occupy the largest of these three parts.

count_nodes(node, x) function: This function recursively calculates the number of nodes in the left and right subtrees of the node with value x. It traverses the tree and, when it finds the node with value x, it stores the counts of its left and right subtrees in self.left_count and self.right_count respectively.
Calculate Parent Count: After finding the left and right subtree counts, we calculate the number of nodes in the remaining part of the tree (the parent part) by subtracting the total number of nodes in the left and right subtrees of x and x itself from the total number of nodes n.
Check for Winning Move: Finally, we check if any of the three parts (parent, left subtree, right subtree) has more than n // 2 nodes. If it does, the second player can win by choosing a node in that part.

Example

Consider the example where root = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11], n = 11, and x = 3. The tree looks like this:

If the first player chooses node with value 3, the second player can choose node with value 2. The left subtree of 3 has 0 nodes, the right subtree has 0 nodes and the parent has 9 nodes. If we chose node 2, it has a left subtree with 3 nodes, right subtree with 3 nodes and parent 1 node. In total, node 2 has a winning move of capturing the 6 nodes in its subtrees, letting it win.

Big(O) Run-time Analysis

The count_nodes function traverses the entire tree once in the worst case. Therefore, the time complexity is O(n), where n is the number of nodes in the tree.

Big(O) Space Usage Analysis

The space complexity is determined by the recursion depth of the count_nodes function. In the worst case, the tree is skewed, and the recursion depth can be n. Therefore, the space complexity is O(n).

Edge Cases

Empty Tree: If the tree is empty (root is None), the function should return False because the game cannot be played.
Single Node Tree: If the tree has only one node (n = 1), the function should return False because the first player cannot choose a value x such that 1 <= x <= n.
x is root: When x is the root node, the parent_count would be zero and the condition would depend on the sizes of left and right subtrees.
n = 3: When n = 3, if x = 1 then it is not possible for player 2 to win. When x = 2, the tree could be represented as [1,2,3], the parent of x is None. Player 2 can chose 1 or 3. left_count = 0, right_count = 0 and parent count = 2.