Insertion Sort List

Given the head of a singly linked list, sort the list using insertion sort, and return the sorted list's head.

The steps of the insertion sort algorithm:

1. Insertion sort iterates, consuming one input element each repetition and growing a sorted output list.
2. At each iteration, insertion sort removes one element from the input data, finds the location it belongs within the sorted list and inserts it there.
3. It repeats until no input elements remain.

The following is a graphical example of the insertion sort algorithm. The partially sorted list (black) initially contains only the first element in the list. One element (red) is removed from the input data and inserted in-place into the sorted list with each iteration.

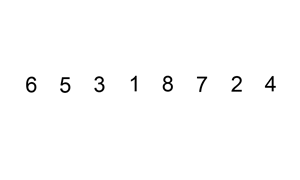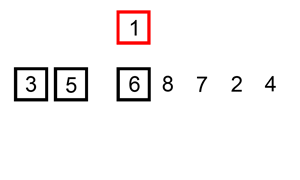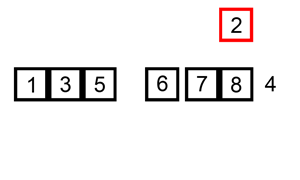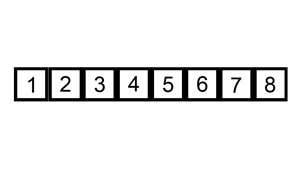
Example 1:

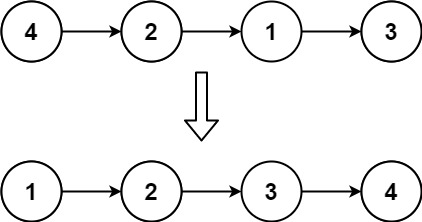
Input: head = [4,2,1,3]
Output: [1,2,3,4]

Example 2:

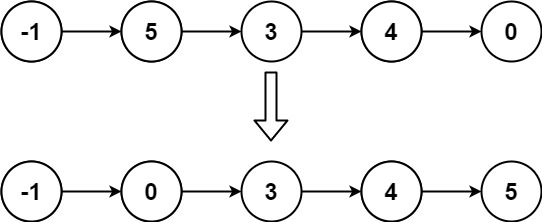
Input: head = [-1,5,3,4,0]
Output: [-1,0,3,4,5]

Constraints:

• The number of nodes in the list is in the range [1, 5000].
• -5000 <= Node.val <= 5000

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, val=0, next=None):
#         self.val = val
#         self.next = next
class Solution:
    def insertionSortList(self, head: Optional[ListNode]) -> Optional[ListNode]:
        dummy = ListNode(0)
        dummy.next = head
        
        current = head
        while current and current.next:
            if current.val <= current.next.val:
                current = current.next
            else:
                # Remove current.next
                node_to_insert = current.next
                current.next = current.next.next
                
                # Find the right position to insert
                prev = dummy
                while prev.next and prev.next.val < node_to_insert.val:
                    prev = prev.next
                
                # Insert the node
                node_to_insert.next = prev.next
                prev.next = node_to_insert
        
        return dummy.next

Explanation:

The insertion sort algorithm works by iterating through the list and inserting each element into its correct position in a sorted sublist.

1. Initialize a Dummy Node:

• A dummy node is created to simplify the insertion process, especially when inserting at the beginning of the list.

1. Iterate Through the List:

• The current pointer starts at the head of the list and moves through the list.
• If the current node's value is less than or equal to the next node's value, the list is already sorted in that section, so current moves to the next node.
• If the current node's value is greater than the next node's value, the next node needs to be inserted into the correct position in the sorted sublist.

1. Insertion Process:

• The node to be inserted (node_to_insert) is current.next.
• current.next is updated to skip over node_to_insert.
• A prev pointer starts at the dummy node and moves through the sorted sublist until it finds the correct position to insert node_to_insert.
• node_to_insert is inserted into the correct position by updating the next pointers of node_to_insert and prev.

1. Repeat:

• The process repeats until the end of the list is reached.

1. Return the Sorted List:

• The next pointer of the dummy node points to the head of the sorted list, which is returned.

Example:

Let's walk through an example to illustrate the process. Suppose we have the following linked list:

4 -> 2 -> 1 -> 3

1. Initial state: dummy -> 4 -> 2 -> 1 -> 3, current = 4

2. 4 > 2, so we need to insert 2 into the sorted sublist dummy -> 4.

• node_to_insert = 2
• current.next = 1
• Find the correct position to insert 2: dummy -> 4, prev = dummy
• Insert 2: dummy -> 2 -> 4 -> 1 -> 3
• current = 4

1. 4 > 1, so we need to insert 1 into the sorted sublist dummy -> 2 -> 4.

• node_to_insert = 1
• current.next = 3
• Find the correct position to insert 1: dummy -> 2 -> 4, prev = dummy
• Insert 1: dummy -> 1 -> 2 -> 4 -> 3
• current = 4

1. 4 > 3, so we need to insert 3 into the sorted sublist dummy -> 1 -> 2 -> 4.

• node_to_insert = 3
• current.next = None
• Find the correct position to insert 3: dummy -> 1 -> 2 -> 4, prev = dummy -> 1 -> 2
• Insert 3: dummy -> 1 -> 2 -> 3 -> 4
• current = 4

1. The list is now sorted: 1 -> 2 -> 3 -> 4

Big O Runtime Analysis

The outer while loop iterates through each element in the linked list, resulting in O(n) complexity. For each element, there is an inner while loop that iterates through the sorted portion of the linked list to find the correct insertion point. In the worst-case scenario, the inner while loop might have to iterate through all the elements in the sorted portion, which could be up to n elements. Therefore, the overall time complexity is O(n^2).

Big O Space Usage Analysis

The space complexity of this algorithm is O(1) because it only uses a constant amount of extra space to store the dummy node and the current, prev, and node_to_insert pointers. The algorithm sorts the linked list in place, without creating any additional data structures that scale with the size of the input.