Angle Between Hands of a Clock

Given two numbers, hour and minutes, return the smaller angle (in degrees) formed between the hour and the minute hand.

Answers within 10-5 of the actual value will be accepted as correct.

Example 1:

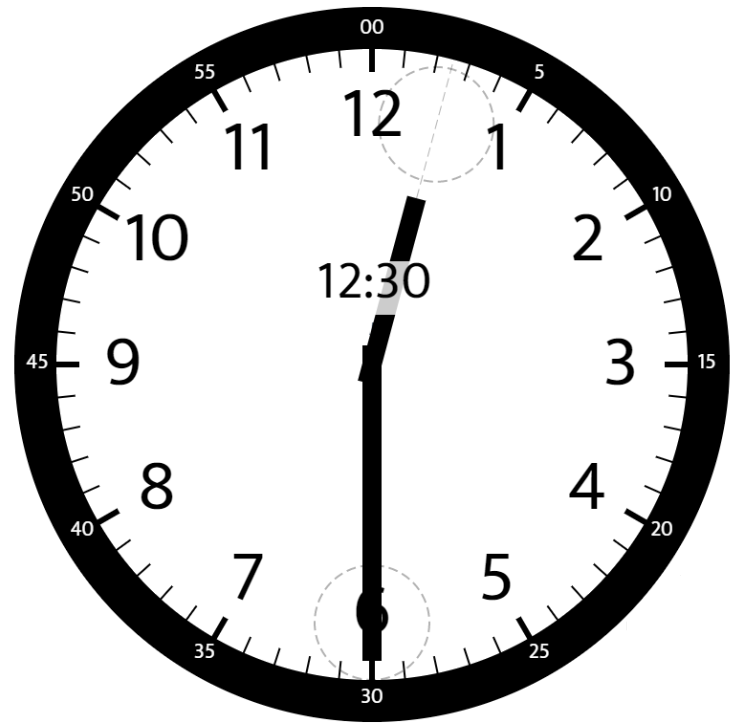
Input: hour = 12, minutes = 30
Output: 165

Example 2:

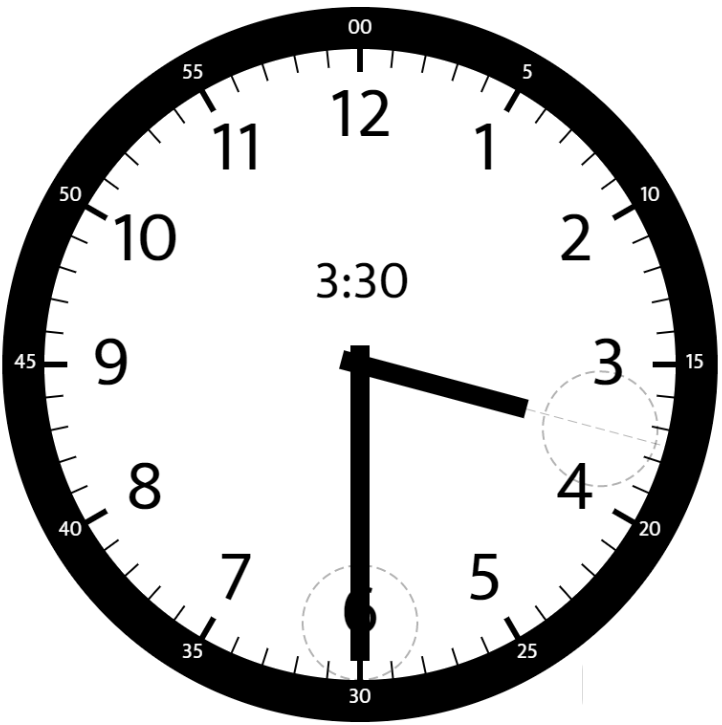
Input: hour = 3, minutes = 30
Output: 75

Example 3:

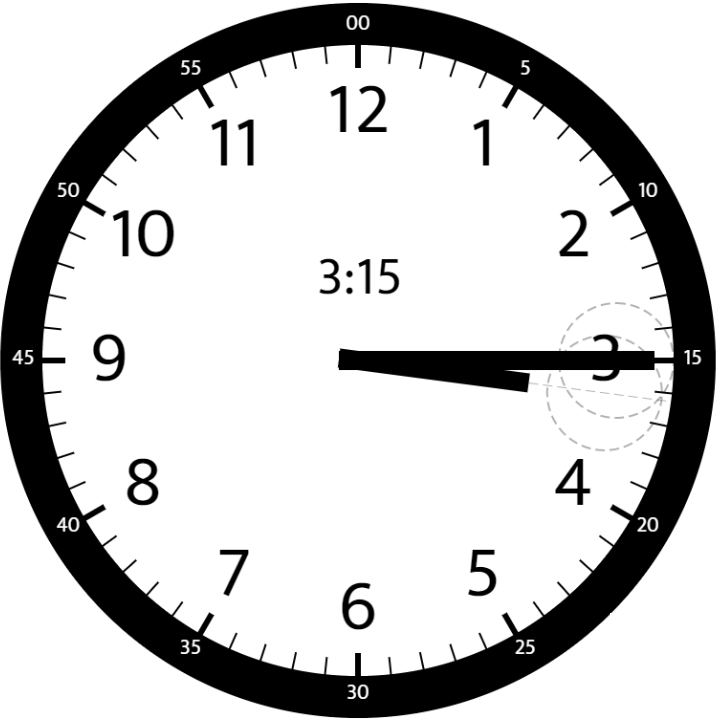
Input: hour = 3, minutes = 15
Output: 7.5

Constraints:

• 1 <= hour <= 12
• 0 <= minutes <= 59

def angleClock(hour: int, minutes: int) -> float:
    """Calculates the smaller angle between the hour and minute hands on a clock.

    Args:
        hour: The hour (1-12).
        minutes: The minutes (0-59).

    Returns:
        The smaller angle in degrees between the hour and minute hands.
    """
    # Calculate the angle of the hour hand
    hour_angle = (hour % 12 + minutes / 60) * 30

    # Calculate the angle of the minute hand
    minute_angle = minutes * 6

    # Calculate the absolute difference between the angles
    angle_diff = abs(hour_angle - minute_angle)

    # Return the smaller angle
    return min(angle_diff, 360 - angle_diff)

# Example usage:
# print(angleClock(12, 30))
# print(angleClock(3, 30))
# print(angleClock(3, 15))

Naive Approach

The most straightforward way to solve this problem is to directly calculate the angles of the hour and minute hands and then find the difference. This involves:

1. Calculating the angle of the hour hand based on the hour and minute values.
2. Calculating the angle of the minute hand based on the minute value.
3. Finding the absolute difference between the two angles.
4. Returning the smaller angle between the difference and its complement (360 - difference).

Optimal Solution

The provided Python code implements the optimal solution, which is essentially a refined version of the naive approach. Here's a breakdown:

1. Hour Hand Angle Calculation: The hour hand moves 30 degrees per hour (360/12) and also moves a fraction of 30 degrees based on the minutes. Thus, the formula (hour % 12 + minutes / 60) * 30 accurately calculates the hour hand's angle.
2. Minute Hand Angle Calculation: The minute hand moves 6 degrees per minute (360/60). Thus, the formula minutes * 6 calculates the minute hand's angle.
3. Angle Difference: The absolute difference between the two angles is calculated using abs(hour_angle - minute_angle).
4. Smaller Angle: The final result is the smaller of angle_diff and 360 - angle_diff, ensuring the smallest angle between the hands is returned.

Big(O) Run-Time Analysis

The run-time complexity of the angleClock function is O(1) because it involves only a few arithmetic operations that take constant time regardless of the input values. Specifically:

• Calculating hour_angle involves a fixed number of arithmetic operations.
• Calculating minute_angle involves a single multiplication.
• Calculating angle_diff involves a subtraction and an absolute value operation.
• Finding the minimum angle involves a comparison.

Since all these operations take constant time, the overall run-time complexity is O(1).

Big(O) Space Usage Analysis

The space complexity of the angleClock function is O(1) because it uses a fixed amount of memory regardless of the input values. Specifically:

• A few variables (hour_angle, minute_angle, angle_diff) are used to store intermediate results, but the number of variables does not depend on the input.

Since the memory usage remains constant, the space complexity is O(1).

Edge Cases and Handling

1. Hour Value of 12: The modulo operator % 12 ensures that when the hour is 12, it is treated as 0 for angle calculation purposes, which is correct.
2. Minutes Value of 60: The problem statement constrains minutes to be between 0 and 59, so there is no need to handle a minutes value of 60 or more.
3. Negative Angle Difference: The abs() function ensures that the angle difference is always positive, simplifying the logic for finding the smaller angle.
4. Floating Point Precision: The problem statement specifies that answers within 10^-5 of the actual value will be accepted, which means the floating-point calculations are precise enough for the problem requirements. No special handling is needed for floating-point precision issues.

This approach effectively handles all valid inputs within the constraints specified by the problem statement.