Design Skiplist

Design a Skiplist without using any built-in libraries.

A skiplist is a data structure that takes O(log(n)) time to add, erase and search. Comparing with treap and red-black tree which has the same function and performance, the code length of Skiplist can be comparatively short and the idea behind Skiplists is just simple linked lists.

For example, we have a Skiplist containing [30,40,50,60,70,90] and we want to add 80 and 45 into it. The Skiplist works this way:

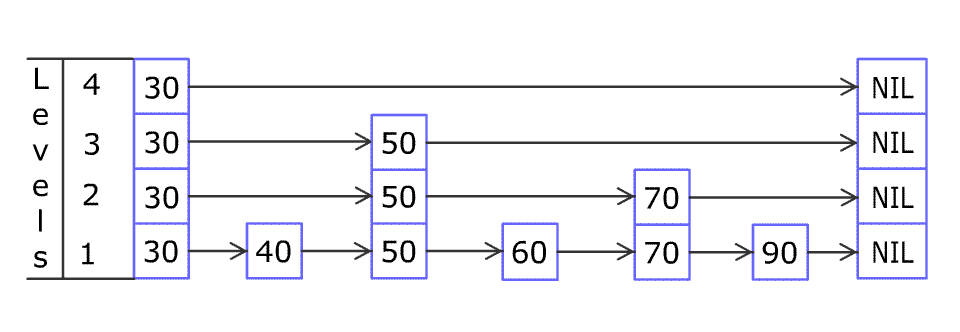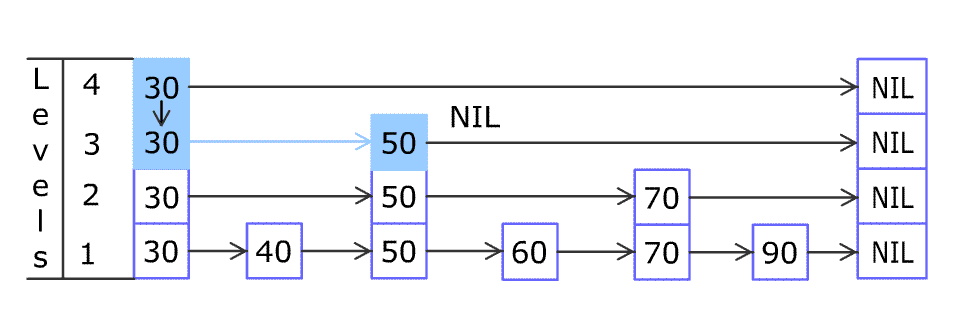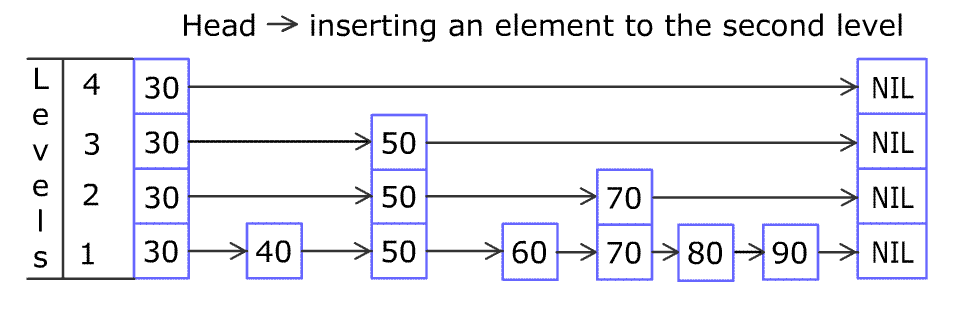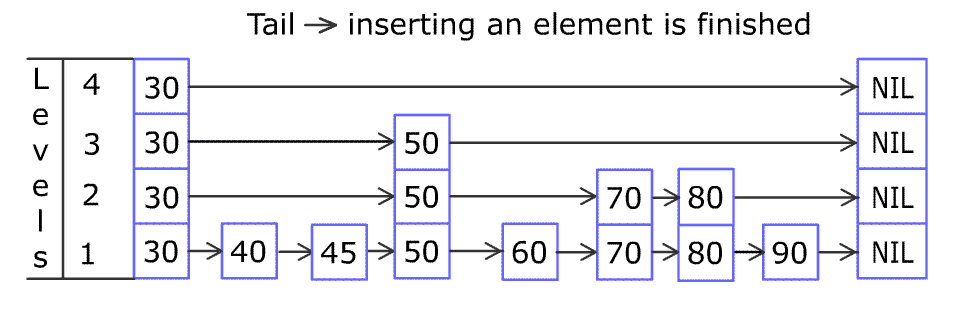
Artyom Kalinin [CC BY-SA 3.0], via Wikimedia Commons

You can see there are many layers in the Skiplist. Each layer is a sorted linked list. With the help of the top layers, add, erase and search can be faster than O(n). It can be proven that the average time complexity for each operation is O(log(n)) and space complexity is O(n).

See more about Skiplist: https://en.wikipedia.org/wiki/Skip_list

Implement the Skiplist class:

• Skiplist() Initializes the object of the skiplist.
• bool search(int target) Returns true if the integer target exists in the Skiplist or false otherwise.
• void add(int num) Inserts the value num into the SkipList.
• bool erase(int num) Removes the value num from the Skiplist and returns true. If num does not exist in the Skiplist, do nothing and return false. If there exist multiple num values, removing any one of them is fine.

Note that duplicates may exist in the Skiplist, your code needs to handle this situation.

Example 1:

 Input ["Skiplist", "add", "add", "add", "search", "add", "search", "erase", "erase", "search"] [[], [1], [2], [3], [0], [4], [1], [0], [1], [1]] Output [null, null, null, null, false, null, true, false, true, false] Explanation Skiplist skiplist = new Skiplist(); skiplist.add(1); skiplist.add(2); skiplist.add(3); skiplist.search(0); // return False skiplist.add(4); skiplist.search(1); // return True skiplist.erase(0); // return False, 0 is not in skiplist. skiplist.erase(1); // return True skiplist.search(1); // return False, 1 has already been erased.

Constraints:

• 0 <= num, target <= 2 * 104
• At most 5 * 104 calls will be made to search, add, and erase.

## Skiplist Implementation in Python

Here's a Python implementation of a Skiplist data structure without using any built-in libraries, along with explanations, complexity analysis, and edge case handling.

### Naive Solution (Sorted List)

Before diving into the Skiplist, let's consider a naive approach using a simple sorted list.  This allows for `O(n)` search, insert, and delete operations.

```python
class SortedList:
    def __init__(self):
        self.items = []

    def search(self, target):
        return target in self.items

    def add(self, num):
        self.items.append(num)
        self.items.sort()

    def erase(self, num):
        if num in self.items:
            self.items.remove(num)
            return True
        return False

This approach is simple but inefficient for large datasets.

Optimal Solution: Skiplist

import random

class Node:
    def __init__(self, val, level):
        self.val = val
        self.forward = [None] * (level + 1)

class Skiplist:
    def __init__(self, max_level=16, p=0.5):
        self.max_level = max_level
        self.p = p
        self.level = 0
        self.head = Node(-1, max_level)

    def random_level(self):
        level = 0
        while random.random() < self.p and level < self.max_level:
            level += 1
        return level

    def search(self, target):
        node = self.head
        for i in range(self.level, -1, -1):
            while node.forward[i] and node.forward[i].val < target:
                node = node.forward[i]
        if node.forward[0] and node.forward[0].val == target:
            return True
        return False

    def add(self, num):
        update = [None] * (self.max_level + 1)
        node = self.head
        for i in range(self.level, -1, -1):
            while node.forward[i] and node.forward[i].val < num:
                node = node.forward[i]
            update[i] = node

        level = self.random_level()
        if level > self.level:
            for i in range(self.level + 1, level + 1):
                update[i] = self.head
            self.level = level

        new_node = Node(num, level)
        for i in range(level + 1):
            new_node.forward[i] = update[i].forward[i]
            update[i].forward[i] = new_node

    def erase(self, num):
        update = [None] * (self.max_level + 1)
        node = self.head
        for i in range(self.level, -1, -1):
            while node.forward[i] and node.forward[i].val < num:
                node = node.forward[i]
            update[i] = node

        if node.forward[0] and node.forward[0].val == num:
            node_to_delete = node.forward[0]
            for i in range(self.level + 1):
                if update[i].forward[i] != node_to_delete:
                    break
                update[i].forward[i] = node_to_delete.forward[i]

            while self.level > 0 and self.head.forward[self.level] is None:
                self.level -= 1
            return True
        return False

Big(O) Runtime Analysis

• Search: O(log n) on average. The skiplist allows us to skip over elements, similar to binary search. In the worst case (very poorly constructed skiplist), it can degrade to O(n).
• Add: O(log n) on average. Finding the correct position to insert takes O(log n), and the insertion itself takes constant time per level. The random level generation is independent of n.
• Erase: O(log n) on average. Similar to add, finding the element to erase takes O(log n), and updating the pointers takes constant time per level.

Big(O) Space Usage Analysis

• Skiplist: O(n). Each element is stored once in the bottom layer, and on average, a fraction 'p' of the elements are also stored in the layer above, and so on. This results in an average space complexity of O(n).

Edge Cases and Handling

1. Empty Skiplist: The code handles the case when the skiplist is initially empty. The search function will correctly return False, and the add function will create the first node.
2. Duplicates: The code handles duplicate values correctly. search will return true if the target exists, even if there are multiple instances. erase will remove only one instance of the value.
3. Target Smaller than Minimum Value: The search function correctly returns False if the target is smaller than the smallest value in the skiplist.
4. Target Larger than Maximum Value: The search function correctly returns False if the target is larger than the largest value in the skiplist.
5. Emptying the Skiplist: The erase function correctly updates the level of the skiplist as elements are removed, ensuring that the skiplist doesn't have unnecessary layers.

Example Usage

skiplist = Skiplist()
skiplist.add(1)
skiplist.add(2)
skiplist.add(3)
print(skiplist.search(0))  # Output: False
skiplist.add(4)
print(skiplist.search(1))  # Output: True
print(skiplist.erase(0))   # Output: False
print(skiplist.erase(1))   # Output: True
print(skiplist.search(1))  # Output: False

Explanation of Key Concepts

• Levels: The skiplist consists of multiple levels of linked lists. The bottom level contains all the elements, and higher levels contain a subset of the elements. Higher levels act as