Longest Absolute File Path Interview Question for Meta

Suppose we have a file system that stores both files and directories. An example of one system is represented in the following picture:

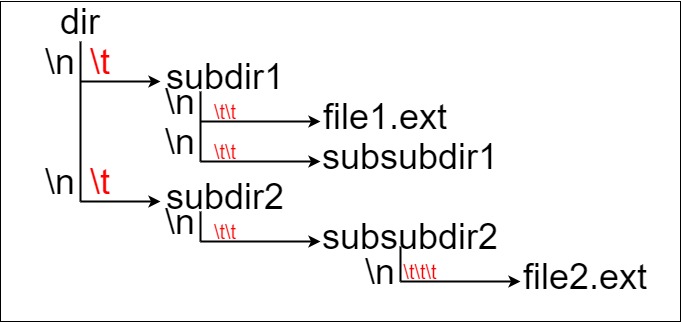
Here, we have dir as the only directory in the root. dir contains two subdirectories, subdir1 and subdir2. subdir1 contains a file file1.ext and subdirectory subsubdir1. subdir2 contains a subdirectory subsubdir2, which contains a file file2.ext.

In text form, it looks like this (with ⟶ representing the tab character):

dir
⟶ subdir1
⟶ ⟶ file1.ext
⟶ ⟶ subsubdir1
⟶ subdir2
⟶ ⟶ subsubdir2
⟶ ⟶ ⟶ file2.ext

If we were to write this representation in code, it will look like this: "dir\n\tsubdir1\n\t\tfile1.ext\n\t\tsubsubdir1\n\tsubdir2\n\t\tsubsubdir2\n\t\t\tfile2.ext". Note that the '\n' and '\t' are the new-line and tab characters.

Every file and directory has a unique absolute path in the file system, which is the order of directories that must be opened to reach the file/directory itself, all concatenated by '/'s. Using the above example, the absolute path to file2.ext is "dir/subdir2/subsubdir2/file2.ext". Each directory name consists of letters, digits, and/or spaces. Each file name is of the form name.extension, where name and extension consist of letters, digits, and/or spaces.

Given a string input representing the file system in the explained format, return the length of the longest absolute path to a file in the abstracted file system. If there is no file in the system, return 0.

Note that the testcases are generated such that the file system is valid and no file or directory name has length 0.

For example, given the input "dir\n\tsubdir1\n\tsubdir2\n\t\tfile.ext", the output should be 20 because the longest absolute path is "dir/subdir2/file.ext". Given the input "dir\n\tsubdir1\n\t\tfile1.ext\n\t\tsubsubdir1\n\tsubdir2\n\t\tsubsubdir2\n\t\t\tfile2.ext", the output should be 32 because the longest absolute path is "dir/subdir2/subsubdir2/file2.ext". What is the time and space complexity of your solution?

def lengthLongestPath(input):
    """
    Calculates the length of the longest absolute path to a file in the abstracted file system.

    Args:
        input (str): A string representing the file system.

    Returns:
        int: The length of the longest absolute path to a file.
    """
    max_length = 0
    path_lengths = {0: 0}
    for line in input.splitlines():
        name = line.lstrip('\t')
        depth = len(line) - len(name)
        if '.' in name:
            max_length = max(max_length, path_lengths[depth] + len(name))
        else:
            path_lengths[depth + 1] = path_lengths[depth] + len(name) + 1
    return max_length

# Example Usage
input1 = "dir\n\tsubdir1\n\tsubdir2\n\t\tfile.ext"
print(f"Longest path for input1: {lengthLongestPath(input1)}")

input2 = "dir\n\tsubdir1\n\t\tfile1.ext\n\t\tsubsubdir1\n\tsubdir2\n\t\tsubsubdir2\n\t\t\tfile2.ext"
print(f"Longest path for input2: {lengthLongestPath(input2)}")

input3 = "a"
print(f"Longest path for input3: {lengthLongestPath(input3)}")

input4 = "file1.txt\nfile2.txt"
print(f"Longest path for input4: {lengthLongestPath(input4)}")

input5 = "dir\n\tfile.txt"
print(f"Longest path for input5: {lengthLongestPath(input5)}")

Explanation:

Initialization:
- max_length: Initialized to 0. This variable will store the maximum length found so far.
- path_lengths: A dictionary initialized with {0: 0}. This dictionary stores the path length up to each level. The root level (0) has a path length of 0.
Iterating Through Lines:
- The code iterates through each line of the input string using input.splitlines(). Each line represents a file or directory.
Determining Depth and Name:
- name = line.lstrip('\t'): Removes leading tab characters from the line to get the name of the file or directory.
- depth = len(line) - len(name): Calculates the depth of the file or directory by counting the number of leading tabs. Each tab represents one level of depth.
Checking for File:
- if '.' in name:: Checks if the name contains a . character, which indicates that it's a file.
  - If it's a file, the code calculates the full path length by adding the path length of the parent directory (path_lengths[depth]) to the length of the file name (len(name)). It then updates max_length with the maximum length found so far.
Handling Directories:
- else:: If the name does not contain a ., it's a directory.
  - path_lengths[depth + 1] = path_lengths[depth] + len(name) + 1: Calculates the path length for the next level (depth + 1). It adds the path length of the current directory (path_lengths[depth]), the length of the directory name (len(name)), and 1 (for the / separator) to get the path length of the next level. This path length is stored in the path_lengths dictionary.
Returning the Result:
- After processing all lines, the code returns the max_length, which represents the length of the longest absolute path to a file.

Example Walkthrough (input1):

input1 = "dir\n\tsubdir1\n\tsubdir2\n\t\tfile.ext"

Initialization:
- max_length = 0
- path_lengths = {0: 0}
Iteration 1: line = "dir"
- name = "dir"
- depth = 0
- The condition '.' in name is false.
- path_lengths[1] = path_lengths[0] + len(name) + 1 = 0 + 3 + 1 = 4. path_lengths becomes {0: 0, 1: 4}
Iteration 2: line = "\tsubdir1"
- name = "subdir1"
- depth = 1
- The condition '.' in name is false.
- path_lengths[2] = path_lengths[1] + len(name) + 1 = 4 + 7 + 1 = 12. path_lengths becomes {0: 0, 1: 4, 2: 12}
Iteration 3: line = "\tsubdir2"
- name = "subdir2"
- depth = 1
- The condition '.' in name is false.
- path_lengths[2] = path_lengths[1] + len(name) + 1 = 4 + 7 + 1 = 12. path_lengths becomes {0: 0, 1: 4, 2: 12}
Iteration 4: line = "\t\tfile.ext"
- name = "file.ext"
- depth = 2
- The condition '.' in name is true.
- max_length = max(0, path_lengths[2] + len(name)) = max(0, 12 + 8) = 20
Return:
- The function returns max_length, which is 20.

Time and Space Complexity:

Time Complexity: O(N), where N is the number of lines in the input string. This is because the code iterates through each line once.
Space Complexity: O(M), where M is the maximum depth of the file system. This is because the path_lengths dictionary stores the path length for each level of depth. In the worst case, the depth can be proportional to the number of lines.